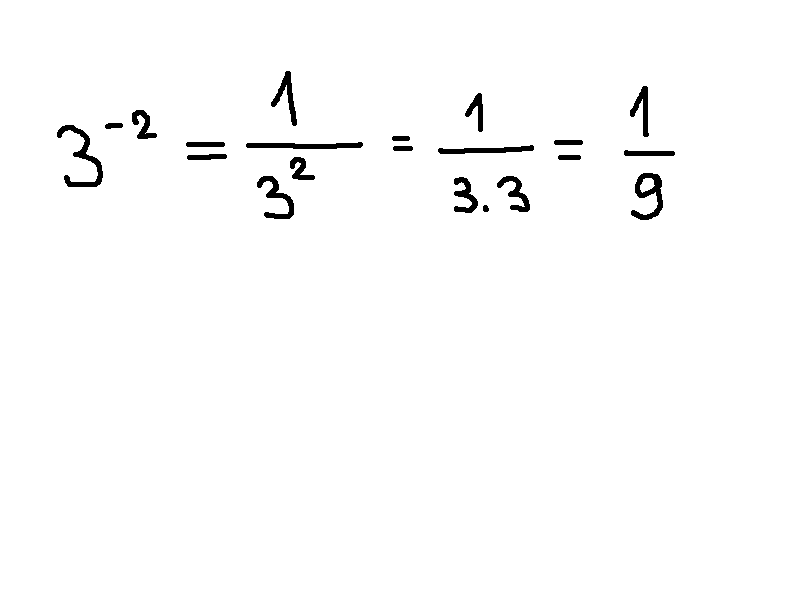GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If a = (27)(3^–2^ ) and x = (6)(3 ^–1^ ), then which of the
[#permalink]
23 May 2017, 02:47
23 May 2017, 02:47
Expert Reply
00:00
Question Stats:
93% (01:22) correct
6% (01:46) wrong based on 189 sessions
Hide Show timer Statistics
If a = \((27)(3^{-2} )\) and x = \((6)(3^{-1} )\), then which of the following is equivalent to \((12)(3^{-x} ) * (15)(2^{-a} )\) ?
A) \(5(-2245)(320)\)
B) \(\frac{2}{5}\)
C) \(\frac{5}{2}\)
D) \(5(24)(38)\)
E) \(5(2245)(320)\)
Re: If a = (27)(3^–2^ ) and x = (6)(3 ^–1^ ), then which of the
[#permalink]
10 Oct 2017, 08:08
10 Oct 2017, 08:08
1
Carcass wrote:
If a = \((27)(3^^{-2} )\) and x = \((6)(3 ^{-1} )\), then which of the following is equivalent to \((12)(3 ^{-x} ) * (15)(2 ^{-a} )\) ?
A) 5(–2245)(320)
B) \(\frac{2}{5}\)
C) \(\frac{5}{2}\)
D) 5(24)(38)
E) 5(2245)(320)
a can be rewritten as \(\frac{27}{9} = 3\) and x as \(\frac{6}{3} = 2\). Then, the expression becomes
\((12)(3 ^{-2} ) * (15)(2 ^{-2} ) = \frac{12}{9}*\frac{15}{4} = \frac{5}{2}\).
Answer C
Re: If a = (27)(3^–2^ ) and x = (6)(3 ^–1^ ), then which of the
[#permalink]
05 Feb 2019, 05:48
05 Feb 2019, 05:48
1
a=3 & x=2
(12)(3−x)∗(15)(2−a)=5/2
Answer is c
(12)(3−x)∗(15)(2−a)=5/2
Answer is c
