
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A weighted coin has a probability p of showing heads. If suc
[#permalink]
 01 Dec 2018, 10:54
01 Dec 2018, 10:54
2
Expert Reply
15
Bookmarks
Question Stats:
 41% (02:17) correct
41% (02:17) correct
 58% (01:54) wrong
58% (01:54) wrong  based on 147 sessions
based on 147 sessions
Hide Show timer Statistics
A weighted coin has a probability p of showing heads. If successive flips are independent, and the probability of getting at least one head in two flips is greater than 0.5, then what could p be?
Indicate all possible values.
A. 0.1
B. 0.2
C. 0.3
D. 0.4
E. 0.6
F. 0.7
Indicate all possible values.
A. 0.1
B. 0.2
C. 0.3
D. 0.4
E. 0.6
F. 0.7
ShowHide Answer
Official Answer
C,D,E,F
Re: A weighted coin has a probability p of showing heads. If suc
[#permalink]
 15 Feb 2020, 11:19
15 Feb 2020, 11:19
3
4
Bookmarks
Official Explanation:
Remember that, to calculate the probability of an "at least" scenario, we use the complement rule. The case we want is (at least one H in two flips). The complement of that is (no H in two flips). If p is the probability of H, then (1 – p) is the probability of T. The probability of two T in two flips would be that squared, and then we would subtract from 1 to find the "at least" probability. In the table below, the first column is the possible values of p, the probability of getting H on a single flip. The second column is the probability of getting T on a single flip. The third column is the probability of getting two T's in a row, i.e. no H in two flips; that is the complement of the "at least" case. The final column is the probability of "at least one H in two flips."
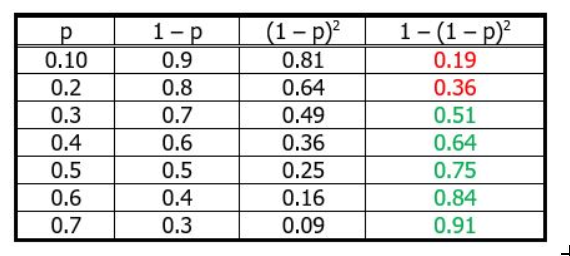
Screenshot from 2020-02-16 01-20-29.png [ 86.07 KiB | Viewed 16630 times ]
We see that for all value of p ≥ 0.3, the "at least" probability is greater than 0.5.
FAQ: Why is the (1 - p) term being squared?
We know that:
P(heads) = p
P(tails) = (1 - p)
This problem ultimately asks us to find the probability of getting "at least one heads in two flips". This means that we want to find the probability of getting the following outcomes:
heads, heads
OR
heads, tails
OR
tails, heads
We can calculate all this more easily by first finding the complement to that. The complement to getting "at least one heads in two flips" is getting "exactly 2 tails":
tails, tails
Thus, we're looking for the probability of getting tails AND tails:
P(exactly 2 tails) = P(tails) * P(tails) = P(tails)^2
Substituting in for the value of P(tails), we get:
P(exactly 2 tails) = (1 - p)^2
Taking the complement of this gives us the final expression for our chart:
P(at least one heads) = 1 - P(exactly 2 tails)
P(at least one heads) = 1 - (1 - p)^2
FAQ: Do we really have to make that whole chart? That would take too long!
No, you don't have to fill in that whole chart. That's just being used to illustrate the thinking behind this problem. To solve the problem, you really only need to know that expression in the last column: 1 - (1 - p)^2. We know that that expression must be greater than 0.5. So we end up with:
1 - (1 - p)^2 > 0.5
Now you can just plug in the different answer choices as the value for p in this expression and see which values yield a true statement.
Remember that, to calculate the probability of an "at least" scenario, we use the complement rule. The case we want is (at least one H in two flips). The complement of that is (no H in two flips). If p is the probability of H, then (1 – p) is the probability of T. The probability of two T in two flips would be that squared, and then we would subtract from 1 to find the "at least" probability. In the table below, the first column is the possible values of p, the probability of getting H on a single flip. The second column is the probability of getting T on a single flip. The third column is the probability of getting two T's in a row, i.e. no H in two flips; that is the complement of the "at least" case. The final column is the probability of "at least one H in two flips."
Attachment:
Screenshot from 2020-02-16 01-20-29.png [ 86.07 KiB | Viewed 16630 times ]
We see that for all value of p ≥ 0.3, the "at least" probability is greater than 0.5.
FAQ: Why is the (1 - p) term being squared?
We know that:
P(heads) = p
P(tails) = (1 - p)
This problem ultimately asks us to find the probability of getting "at least one heads in two flips". This means that we want to find the probability of getting the following outcomes:
heads, heads
OR
heads, tails
OR
tails, heads
We can calculate all this more easily by first finding the complement to that. The complement to getting "at least one heads in two flips" is getting "exactly 2 tails":
tails, tails
Thus, we're looking for the probability of getting tails AND tails:
P(exactly 2 tails) = P(tails) * P(tails) = P(tails)^2
Substituting in for the value of P(tails), we get:
P(exactly 2 tails) = (1 - p)^2
Taking the complement of this gives us the final expression for our chart:
P(at least one heads) = 1 - P(exactly 2 tails)
P(at least one heads) = 1 - (1 - p)^2
FAQ: Do we really have to make that whole chart? That would take too long!
No, you don't have to fill in that whole chart. That's just being used to illustrate the thinking behind this problem. To solve the problem, you really only need to know that expression in the last column: 1 - (1 - p)^2. We know that that expression must be greater than 0.5. So we end up with:
1 - (1 - p)^2 > 0.5
Now you can just plug in the different answer choices as the value for p in this expression and see which values yield a true statement.
General Discussion
Re: A weighted coin has a probability p of showing heads. If suc
[#permalink]
 04 Dec 2018, 06:34
04 Dec 2018, 06:34
3
Carcass wrote:
A weighted coin has a probability p of showing heads. If successive flips are independent, and the probability of getting at least one head in two flips is greater than 0.5, then what could p be?
Indicate all possible values.
A. 0.1
B. 0.2
C. 0.3
D. 0.4
E. 0.6
F. 0.7
Indicate all possible values.
A. 0.1
B. 0.2
C. 0.3
D. 0.4
E. 0.6
F. 0.7
Explanation::
Probability of getting one head = 1 - (probability of no head)
Since the events are independent and there are 2 successive flips,
so,
Probability of getting one head = 1 - (probability of no head) (probability of no head) = 1- (probability of no head)^2
Let compare each solution:
A) Probability = 0.1 , probability of getting one head = 1 - (1-0.1)^2 = 0.19 (probability of no head = 1 - probability of getting head)
B) Probability = 0.2 , probability of getting one head = 1 - (1-0.2)^2 = 0.36
C) Probability = 0.3 , probability of getting one head = 1 - (1-0.3)^2 = 0.51
D) Probability = 0.4 , probability of getting one head = 1 - (1-0.4)^2 = 0.64
E) Probability = 0.5 , probability of getting one head = 1 - (1-0.5)^2 = 0.75
F) Probability = 0.6 , probability of getting one head = 1 - (1-0.6)^2 = 0.84
G) Probability = 0.7 , probability of getting one head = 1 - (1-0.7)^2 = 0.91
Hence the options are C,D,E,F,G









