
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
GRE Quant - Coordinate Geometry Lines Theory
[#permalink]
 25 Jun 2020, 13:43
25 Jun 2020, 13:43
1
Expert Reply
2
Bookmarks
Frequency of the concepts tested: Medium
Lines in Coordinate Geometry
In Euclidean geometry, a line is a straight curve. In coordinate geometry, lines in a Cartesian plane can be described algebraically by linear equations and linear functions.
Every straight line in the plane can represented by a first degree equation with two variables.
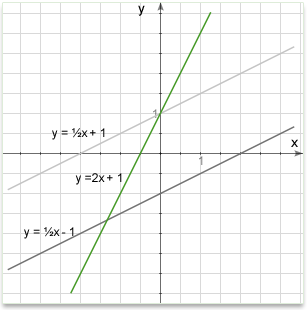
There are several approaches commonly used in coordinate geometry. It does not matter whether we are talking about a line, ray or line segment. In all cases any of the below methods will provide enough information to define the line exactly.
1. General form.
The general form of the equation of a straight line is
\(ax+by+c=0\)
Where \(a\), \(b\) and \(c\) are arbitrary constants. This form includes all other forms as special cases. For an equation in this form the slope is \(-\frac{a}{b}\) and the y intercept is \(-\frac{c}{b}\).
2. Point-intercept form.
\(y=mx+b\)
Where: \(m\) is the slope of the line; \(b\) is the y-intercept of the line; \(x\) is the independent variable of the function \(y\).
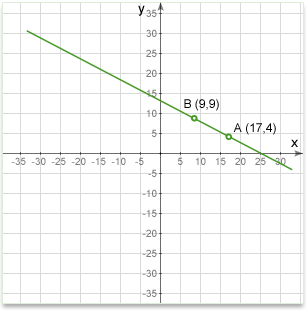
3. Using two points
In figure below, a line is defined by the two points A and B. By providing the coordinates of the two points, we can draw a line. No other line could pass through both these points and so the line they define is unique.
The equation of a straight line passing through points \(P_1(x_1, y_1)\) and \(P_2(x_2, y_2)\) is:
\(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\)
Example #1
Q: Find the equation of a line passing through the points A (17,4) and B (9,9).
Solution: Substituting the values in equation \(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\) we'll get: \(\frac{y-4}{x-17}=\frac{4-9}{17-9}\)
\(\frac{y-4}{x-17}=\frac{-5}{8}\) --> \(8y-32=-5x+85\) --> \(8y+5x-117=0\) OR if we want to write the equation in the slope-intercept form: \(y=-\frac{5}{8}x+\frac{117}{8}\)
4. Using one point and the slope
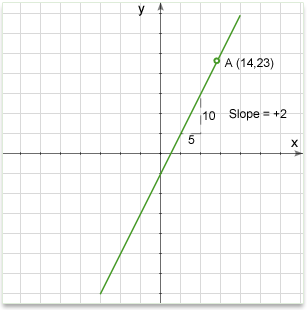
Sometimes on the GMAT you will be given a point on the line and its slope and from this information you will need to find the equation or check if this line goes through another point. You can think of the slope as the direction of the line. So once you know that a line goes through a certain point, and which direction it is pointing, you have defined one unique line.
In figure below, we see a line passing through the point A at (14,23). We also see that it's slope is +2 (which means it goes 2 up for every one across). With these two facts we can establish a unique line.
The equation of a straight line that passes through a point \(P_1(x_1, y_1)\) with a
slope m is:
\(y-y_1=m(x-x_1)\)
Example #2
Q: Find the equation of a line passing through the point A (14,23) and the slope 2.
Solution: Substituting the values in equation \(y-y_1=m(x-x_1)\) we'll get \(y-23=2(x-14)\) --> \(y=2x-5\)
4. Intercept form.
The equation of a straight line whose x and y intercepts are a and b, respectively, is:
\(\frac{x}{a}+\frac{y}{b}=1\)
Example #3
Q: Find the equation of a line whose x intercept is 5 and y intercept is 2.
Solution: Substituting the values in equation \(\frac{x}{a}+\frac{y}{b}=1\) we'll get \(\frac{x}{5}+\frac{y}{2}=1\) --> \(5y+2x-10=0\) OR if we want to write the equation in the slope-intercept form: \(y=-\frac{2}{5}x+2\)
Slope of a Line
The slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline.
The slope is defined as the ratio of the "rise" divided by the "run" between two points on a line, or in other words, the ratio of the altitude change to the horizontal distance between any two points on the line.
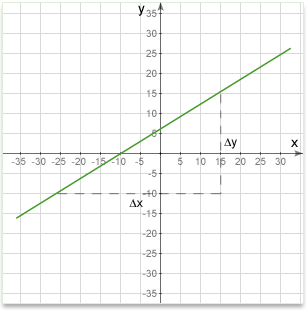
Given two points \((x_1,y_1)\) and \((x_2,y_2)\) on a line, the slope \(m\) of the line is:
\(m=\frac{y_2-y_1}{x_2-x_1}\)
If the equation of the line is given in the Point-intercept form: \(y=mx+b\), then \(m\) is the slope. This form of a line's equation is called the slope-intercept form, because \(b\) can be interpreted as the y-intercept of the line, the y-coordinate where the line intersects the y-axis.
If the equation of the line is given in the General form:\(ax+by+c=0\), then the slope is \(-\frac{a}{b}\) and the y intercept is \(-\frac{c}{b}\).
SLOPE DIRECTION
The slope of a line can be positive, negative, zero or undefined.
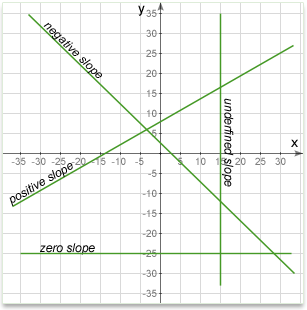
Positive slope
Here, y increases as x increases, so the line slopes upwards to the right. The slope will be a positive number. The line below has a slope of about +0.3, it goes up about 0.3 for every step of 1 along the x-axis.
Negative slope
Here, y decreases as x increases, so the line slopes downwards to the right. The slope will be a negative number. The line below has a slope of about -0.3, it goes down about 0.3 for every step of 1 along the x-axis.
Zero slope
Here, y does not change as x increases, so the line in exactly horizontal. The slope of any horizontal line is always zero. The line below goes neither up nor down as x increases, so its slope is zero.
Undefined slope
When the line is exactly vertical, it does not have a defined slope. The two x coordinates are the same, so the difference is zero. The slope calculation is then something like \(slope=\frac{15}{0}\) When you divide anything by zero the result has no meaning. The line above is exactly vertical, so it has no defined slope.
SLOPE AND QUADRANTS:
1. If the slope of a line is negative, the line WILL intersect quadrants II and IV. X and Y intercepts of the line with negative slope have the same sign. Therefore if X and Y intersects are positive, the line intersects quadrant I; if negative, quadrant III.
2. If the slope of line is positive, line WILL intersect quadrants I and III. Y and X intercepts of the line with positive slope have opposite signs. Therefore if X intersect is negative, line intersects the quadrant II too, if positive quadrant IV.
3. Every line (but the one crosses origin OR parallel to X or Y axis OR X and Y axis themselves) crosses three quadrants. Only the line which crosses origin \((0,0)\) OR is parallel to either of axis crosses only two quadrants.
4. If a line is horizontal it has a slope of \(0\), is parallel to X-axis and crosses quadrant I and II if the Y intersect is positive OR quadrants III and IV, if the Y intersect is negative. Equation of such line is y=b, where b is y intersect.
5. If a line is vertical, the slope is not defined, line is parallel to Y-axis and crosses quadrant I and IV, if the X intersect is positive and quadrant II and III, if the X intersect is negative. Equation of such line is \(x=a\), where a is x-intercept.
6. For a line that crosses two points \((x_1,y_1)\) and \((x_2,y_2)\), slope \(m=\frac{y_2-y_1}{x_2-x_1}\)
7. If the slope is 1 the angle formed by the line is \(45\) degrees.
8. Given a point and slope, equation of a line can be found. The equation of a straight line that passes through a point \((x_1, y_1)\) with a slope \(m\) is: \(y - y_1 = m(x - x_1)\)
Vertical and horizontal lines
A vertical line is parallel to the y-axis of the coordinate plane. All points on the line will have the same x-coordinate.
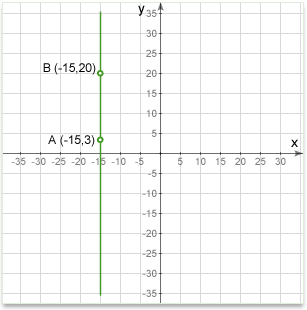
A vertical line has no slope. Or put another way, for a vertical line the slope is undefined.
The equation of a vertical line is:
\(x=a\)
Where: x is the coordinate of any point on the line; a is where the line crosses the x-axis (x intercept). Notice that the equation is independent of y. Any point on the vertical line satisfies the equation.
A horizontal line is parallel to the x-axis of the coordinate plane. All points on the line will have the same y-coordinate.
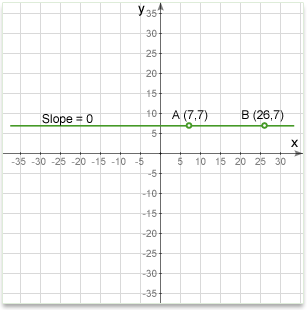
A horizontal line has a slope of zero.
The equation of a horizontal line is:
\(y=b\)
Where: y is the coordinate of any point on the line; b is where the line crosses the y-axis (y intercept). Notice that the equation is independent of x. Any point on the horizontal line satisfies the equation.
Parallel lines
Parallel lines have the same slope.
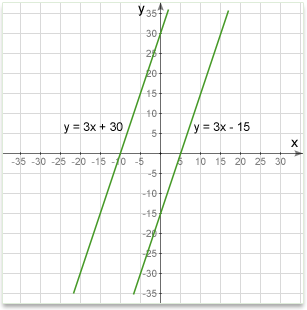
The slope can be found using any method that is convenient to you:
From two given points on the line.
From the equation of the line in slope-intercept form
From the equation of the line in point-slope form
The equation of a line through the point \(P_1(x_1, y_1)\) and parallel to line \(ax + by + c = 0\) is:
\(a(x - x_1) + b(y - y_1) = 0\)
Distance between two parallel lines \(y=mx+b\) and \(y=mx+c\) can be found by the formula:
\(D=\frac{|b-c|}{\sqrt{m^2+1}}\)
Example #1
Q:There are two lines. One line is defined by two points at (5,5) and (25,15). The other is defined by an equation in slope-intercept form form y = 0.52x - 2.5. Are two lines parallel?
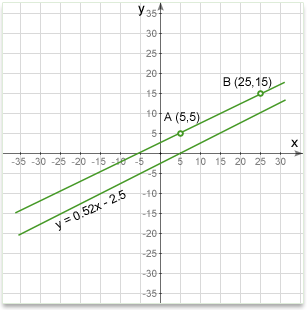
Solution:
For the top line, the slope is found using the coordinates of the two points that define the line. \(Slope=\frac{15-5}{25-5}=0.5\)
For the lower line, the slope is taken directly from the formula. Recall that the slope intercept formula is y = mx + b, where m is the slope. So looking at the formula we see that the slope is 0.52.
So, the top one has a slope of 0.5, the lower slope is 0.52, which are not equal. Therefore, the lines are not parallel.
Example #2
Q: Define a line through a point C parallel to a line passes through the points A and B.
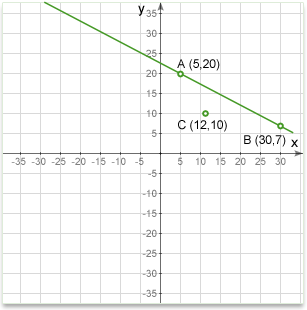
Solution: We first find the slope of the line AB using the same method as in the example above.
\(Slope AB=\frac{20-7}{5-30}=-0.52\)
For the line to be parallel to AB it will have the same slope, and will pass through a given point, C(12,10). We therefore have enough information to define the line by it's equation in point-slope form form:
\(y=-0.52(x-12)+10\) --> \(y=-0.52x+16.24\)
Perpendicular lines
For one line to be perpendicular to another, the relationship between their slopes has to be negative reciprocal \(-\frac{1}{m}\). In other words, the two lines are perpendicular if and only if the product of their slopes is \(-1\).
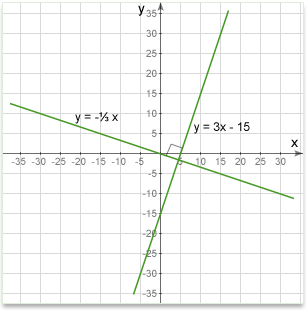
The two lines \(a_1x + b_1y + c_1 = 0\) and \(a_2x + b_2y + c_2 = 0\) are perpendicular if \(a_1a_2 + b_1b_2 = 0\).
The equation of a line passing through the point \(P_1(x_1, y_1\)) and perpendicular to line \(ax + by + c = 0\) is:
\(b(x - x_1)-a(y - y_1) = 0\)
Example #1:
Q: Are the two lines below perpendicular?
Solution:
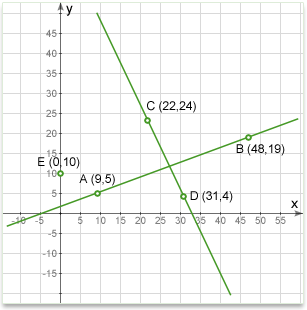
To answer, we must find the slope of each line and then check to see if one slope is the negative reciprocal of the other or if their product equals to -1.
\(Slope AB=\frac{5-19}{9-48}=\frac{-14}{-39}=0.358\)
\(Slope CD=\frac{24-4}{22-31}=\frac{20}{-9}=-2.22\)
If the lines are perpendicular, each will be the negative reciprocal of the other. It doesn't matter which line we start with, so we will pick AB:
Negative reciprocal of 0.358 is \(-\frac{1}{0.358}=-2.79\)
So, the slope of CD is -2.22, and the negative reciprocal of the slope of AB is -2.79. These are not the same, so the lines are not perpendicular, even though they may look as though they are. However, if you looked carefully at the diagram, you might have noticed that point C is a little too far to the left for the lines to be perpendicular.
Example # 2.
Q: Define a line passing through the point E and perpendicular to a line passing through the points C and D on the graph above.
Solution: The point E is on the y-axis and so is the y-intercept of the desired line. Once we know the slope of the line, we can express it using its equation in slope-intercept form y=mx+b, where m is the slope and b is the y-intercept.
First find the slope of line CD:
\(Slope CD=\frac{24-4}{22-31}=\frac{20}{-9}=-2.22\)
The line we seek will have a slope which is the negative reciprocal of:
\(-\frac{1}{-2.22}=0.45\)
Since E is on the Y-axis, we know that the intercept is 10. Plugging these values into the line equation, the line we need is described by the equation
\(y = 0.45x + 10\)
This is one of the ways a line can be defined and so we have solved the problem. If we wanted to plot the line, we would find another point on the line using the equation and then draw the line through that point and the intercept.
Intersection of two straight lines
The point of intersection of two non-parallel lines can be found from the equations of the two lines.
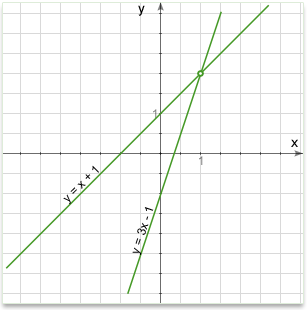
To find the intersection of two straight lines:
1. First we need their equations
2. Then, since at the point of intersection, the two equations will share a point and thus have the same values of x and y, we set the two equations equal to each other. This gives an equation that we can solve for x
3. We substitute the x value in one of the line equations (it doesn't matter which) and solve it for y.
This gives us the x and y coordinates of the intersection.
Example #1
Q: Find the point of intersection of two lines that have the following equations (in slope-intercept form):
\(y = 3x-3\)
\(y = 2.3x+4\)
Solution: At the point of intersection they will both have the same y-coordinate value, so we set the equations equal to each other:
\(3x-3 = 2.3x+4\)
This gives us an equation in one unknown (x) which we can solve:
\(x = 10\)
To find y, simply set x equal to 10 in the equation of either line and solve for y:
Equation for a line \(y = 3x - 3\) (Either line will do)
Set x equal to 10: \(y = 30 - 3\)
\(y = 27\)
We now have both x and y, so the intersection point is (10, 27)
Example #2
Q: Find the point of intersection of two lines that have the following equations (in slope-intercept form): \(y = 3x-3\) and \(x = 12\) (A vertical line)
Solution: When one of the lines is vertical, it has no defined slope. We find the intersection slightly differently.
On the vertical line, all points on it have an x-coordinate of 12 (the definition of a vertical line), so we simply set x equal to 12 in the first equation and solve it for y.
Equation for a line \(y = 3x - 3\)
Set x equal to 12 \(y = 36 - 3\)
\(y = 33\)
So the intersection point is at (12,33).
Note: If both lines are vertical or horizontal, they are parallel and have no intersection
Distance from a point to a line
The distance from a point to a line is the shortest distance between them - the length of a perpendicular line segment from the line to the point.
The distance from a point \((x_0, y_0)\) to a line \(ax+by+c=0\) is given by the formula:
\(D=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
In Euclidean geometry, a line is a straight curve. In coordinate geometry, lines in a Cartesian plane can be described algebraically by linear equations and linear functions.
Every straight line in the plane can represented by a first degree equation with two variables.
There are several approaches commonly used in coordinate geometry. It does not matter whether we are talking about a line, ray or line segment. In all cases any of the below methods will provide enough information to define the line exactly.
1. General form.
The general form of the equation of a straight line is
\(ax+by+c=0\)
Where \(a\), \(b\) and \(c\) are arbitrary constants. This form includes all other forms as special cases. For an equation in this form the slope is \(-\frac{a}{b}\) and the y intercept is \(-\frac{c}{b}\).
2. Point-intercept form.
\(y=mx+b\)
Where: \(m\) is the slope of the line; \(b\) is the y-intercept of the line; \(x\) is the independent variable of the function \(y\).
3. Using two points
In figure below, a line is defined by the two points A and B. By providing the coordinates of the two points, we can draw a line. No other line could pass through both these points and so the line they define is unique.
The equation of a straight line passing through points \(P_1(x_1, y_1)\) and \(P_2(x_2, y_2)\) is:
\(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\)
Example #1
Q: Find the equation of a line passing through the points A (17,4) and B (9,9).
Solution: Substituting the values in equation \(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\) we'll get: \(\frac{y-4}{x-17}=\frac{4-9}{17-9}\)
\(\frac{y-4}{x-17}=\frac{-5}{8}\) --> \(8y-32=-5x+85\) --> \(8y+5x-117=0\) OR if we want to write the equation in the slope-intercept form: \(y=-\frac{5}{8}x+\frac{117}{8}\)
4. Using one point and the slope
Sometimes on the GMAT you will be given a point on the line and its slope and from this information you will need to find the equation or check if this line goes through another point. You can think of the slope as the direction of the line. So once you know that a line goes through a certain point, and which direction it is pointing, you have defined one unique line.
In figure below, we see a line passing through the point A at (14,23). We also see that it's slope is +2 (which means it goes 2 up for every one across). With these two facts we can establish a unique line.
The equation of a straight line that passes through a point \(P_1(x_1, y_1)\) with a
slope m is:
\(y-y_1=m(x-x_1)\)
Example #2
Q: Find the equation of a line passing through the point A (14,23) and the slope 2.
Solution: Substituting the values in equation \(y-y_1=m(x-x_1)\) we'll get \(y-23=2(x-14)\) --> \(y=2x-5\)
4. Intercept form.
The equation of a straight line whose x and y intercepts are a and b, respectively, is:
\(\frac{x}{a}+\frac{y}{b}=1\)
Example #3
Q: Find the equation of a line whose x intercept is 5 and y intercept is 2.
Solution: Substituting the values in equation \(\frac{x}{a}+\frac{y}{b}=1\) we'll get \(\frac{x}{5}+\frac{y}{2}=1\) --> \(5y+2x-10=0\) OR if we want to write the equation in the slope-intercept form: \(y=-\frac{2}{5}x+2\)
Slope of a Line
The slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline.
The slope is defined as the ratio of the "rise" divided by the "run" between two points on a line, or in other words, the ratio of the altitude change to the horizontal distance between any two points on the line.
Given two points \((x_1,y_1)\) and \((x_2,y_2)\) on a line, the slope \(m\) of the line is:
\(m=\frac{y_2-y_1}{x_2-x_1}\)
If the equation of the line is given in the Point-intercept form: \(y=mx+b\), then \(m\) is the slope. This form of a line's equation is called the slope-intercept form, because \(b\) can be interpreted as the y-intercept of the line, the y-coordinate where the line intersects the y-axis.
If the equation of the line is given in the General form:\(ax+by+c=0\), then the slope is \(-\frac{a}{b}\) and the y intercept is \(-\frac{c}{b}\).
SLOPE DIRECTION
The slope of a line can be positive, negative, zero or undefined.
Positive slope
Here, y increases as x increases, so the line slopes upwards to the right. The slope will be a positive number. The line below has a slope of about +0.3, it goes up about 0.3 for every step of 1 along the x-axis.
Negative slope
Here, y decreases as x increases, so the line slopes downwards to the right. The slope will be a negative number. The line below has a slope of about -0.3, it goes down about 0.3 for every step of 1 along the x-axis.
Zero slope
Here, y does not change as x increases, so the line in exactly horizontal. The slope of any horizontal line is always zero. The line below goes neither up nor down as x increases, so its slope is zero.
Undefined slope
When the line is exactly vertical, it does not have a defined slope. The two x coordinates are the same, so the difference is zero. The slope calculation is then something like \(slope=\frac{15}{0}\) When you divide anything by zero the result has no meaning. The line above is exactly vertical, so it has no defined slope.
SLOPE AND QUADRANTS:
1. If the slope of a line is negative, the line WILL intersect quadrants II and IV. X and Y intercepts of the line with negative slope have the same sign. Therefore if X and Y intersects are positive, the line intersects quadrant I; if negative, quadrant III.
2. If the slope of line is positive, line WILL intersect quadrants I and III. Y and X intercepts of the line with positive slope have opposite signs. Therefore if X intersect is negative, line intersects the quadrant II too, if positive quadrant IV.
3. Every line (but the one crosses origin OR parallel to X or Y axis OR X and Y axis themselves) crosses three quadrants. Only the line which crosses origin \((0,0)\) OR is parallel to either of axis crosses only two quadrants.
4. If a line is horizontal it has a slope of \(0\), is parallel to X-axis and crosses quadrant I and II if the Y intersect is positive OR quadrants III and IV, if the Y intersect is negative. Equation of such line is y=b, where b is y intersect.
5. If a line is vertical, the slope is not defined, line is parallel to Y-axis and crosses quadrant I and IV, if the X intersect is positive and quadrant II and III, if the X intersect is negative. Equation of such line is \(x=a\), where a is x-intercept.
6. For a line that crosses two points \((x_1,y_1)\) and \((x_2,y_2)\), slope \(m=\frac{y_2-y_1}{x_2-x_1}\)
7. If the slope is 1 the angle formed by the line is \(45\) degrees.
8. Given a point and slope, equation of a line can be found. The equation of a straight line that passes through a point \((x_1, y_1)\) with a slope \(m\) is: \(y - y_1 = m(x - x_1)\)
Vertical and horizontal lines
A vertical line is parallel to the y-axis of the coordinate plane. All points on the line will have the same x-coordinate.
A vertical line has no slope. Or put another way, for a vertical line the slope is undefined.
The equation of a vertical line is:
\(x=a\)
Where: x is the coordinate of any point on the line; a is where the line crosses the x-axis (x intercept). Notice that the equation is independent of y. Any point on the vertical line satisfies the equation.
A horizontal line is parallel to the x-axis of the coordinate plane. All points on the line will have the same y-coordinate.
A horizontal line has a slope of zero.
The equation of a horizontal line is:
\(y=b\)
Where: y is the coordinate of any point on the line; b is where the line crosses the y-axis (y intercept). Notice that the equation is independent of x. Any point on the horizontal line satisfies the equation.
Parallel lines
Parallel lines have the same slope.
The slope can be found using any method that is convenient to you:
From two given points on the line.
From the equation of the line in slope-intercept form
From the equation of the line in point-slope form
The equation of a line through the point \(P_1(x_1, y_1)\) and parallel to line \(ax + by + c = 0\) is:
\(a(x - x_1) + b(y - y_1) = 0\)
Distance between two parallel lines \(y=mx+b\) and \(y=mx+c\) can be found by the formula:
\(D=\frac{|b-c|}{\sqrt{m^2+1}}\)
Example #1
Q:There are two lines. One line is defined by two points at (5,5) and (25,15). The other is defined by an equation in slope-intercept form form y = 0.52x - 2.5. Are two lines parallel?
Solution:
For the top line, the slope is found using the coordinates of the two points that define the line. \(Slope=\frac{15-5}{25-5}=0.5\)
For the lower line, the slope is taken directly from the formula. Recall that the slope intercept formula is y = mx + b, where m is the slope. So looking at the formula we see that the slope is 0.52.
So, the top one has a slope of 0.5, the lower slope is 0.52, which are not equal. Therefore, the lines are not parallel.
Example #2
Q: Define a line through a point C parallel to a line passes through the points A and B.
Solution: We first find the slope of the line AB using the same method as in the example above.
\(Slope AB=\frac{20-7}{5-30}=-0.52\)
For the line to be parallel to AB it will have the same slope, and will pass through a given point, C(12,10). We therefore have enough information to define the line by it's equation in point-slope form form:
\(y=-0.52(x-12)+10\) --> \(y=-0.52x+16.24\)
Perpendicular lines
For one line to be perpendicular to another, the relationship between their slopes has to be negative reciprocal \(-\frac{1}{m}\). In other words, the two lines are perpendicular if and only if the product of their slopes is \(-1\).
The two lines \(a_1x + b_1y + c_1 = 0\) and \(a_2x + b_2y + c_2 = 0\) are perpendicular if \(a_1a_2 + b_1b_2 = 0\).
The equation of a line passing through the point \(P_1(x_1, y_1\)) and perpendicular to line \(ax + by + c = 0\) is:
\(b(x - x_1)-a(y - y_1) = 0\)
Example #1:
Q: Are the two lines below perpendicular?
Solution:
To answer, we must find the slope of each line and then check to see if one slope is the negative reciprocal of the other or if their product equals to -1.
\(Slope AB=\frac{5-19}{9-48}=\frac{-14}{-39}=0.358\)
\(Slope CD=\frac{24-4}{22-31}=\frac{20}{-9}=-2.22\)
If the lines are perpendicular, each will be the negative reciprocal of the other. It doesn't matter which line we start with, so we will pick AB:
Negative reciprocal of 0.358 is \(-\frac{1}{0.358}=-2.79\)
So, the slope of CD is -2.22, and the negative reciprocal of the slope of AB is -2.79. These are not the same, so the lines are not perpendicular, even though they may look as though they are. However, if you looked carefully at the diagram, you might have noticed that point C is a little too far to the left for the lines to be perpendicular.
Example # 2.
Q: Define a line passing through the point E and perpendicular to a line passing through the points C and D on the graph above.
Solution: The point E is on the y-axis and so is the y-intercept of the desired line. Once we know the slope of the line, we can express it using its equation in slope-intercept form y=mx+b, where m is the slope and b is the y-intercept.
First find the slope of line CD:
\(Slope CD=\frac{24-4}{22-31}=\frac{20}{-9}=-2.22\)
The line we seek will have a slope which is the negative reciprocal of:
\(-\frac{1}{-2.22}=0.45\)
Since E is on the Y-axis, we know that the intercept is 10. Plugging these values into the line equation, the line we need is described by the equation
\(y = 0.45x + 10\)
This is one of the ways a line can be defined and so we have solved the problem. If we wanted to plot the line, we would find another point on the line using the equation and then draw the line through that point and the intercept.
Intersection of two straight lines
The point of intersection of two non-parallel lines can be found from the equations of the two lines.
To find the intersection of two straight lines:
1. First we need their equations
2. Then, since at the point of intersection, the two equations will share a point and thus have the same values of x and y, we set the two equations equal to each other. This gives an equation that we can solve for x
3. We substitute the x value in one of the line equations (it doesn't matter which) and solve it for y.
This gives us the x and y coordinates of the intersection.
Example #1
Q: Find the point of intersection of two lines that have the following equations (in slope-intercept form):
\(y = 3x-3\)
\(y = 2.3x+4\)
Solution: At the point of intersection they will both have the same y-coordinate value, so we set the equations equal to each other:
\(3x-3 = 2.3x+4\)
This gives us an equation in one unknown (x) which we can solve:
\(x = 10\)
To find y, simply set x equal to 10 in the equation of either line and solve for y:
Equation for a line \(y = 3x - 3\) (Either line will do)
Set x equal to 10: \(y = 30 - 3\)
\(y = 27\)
We now have both x and y, so the intersection point is (10, 27)
Example #2
Q: Find the point of intersection of two lines that have the following equations (in slope-intercept form): \(y = 3x-3\) and \(x = 12\) (A vertical line)
Solution: When one of the lines is vertical, it has no defined slope. We find the intersection slightly differently.
On the vertical line, all points on it have an x-coordinate of 12 (the definition of a vertical line), so we simply set x equal to 12 in the first equation and solve it for y.
Equation for a line \(y = 3x - 3\)
Set x equal to 12 \(y = 36 - 3\)
\(y = 33\)
So the intersection point is at (12,33).
Note: If both lines are vertical or horizontal, they are parallel and have no intersection
Distance from a point to a line
The distance from a point to a line is the shortest distance between them - the length of a perpendicular line segment from the line to the point.
The distance from a point \((x_0, y_0)\) to a line \(ax+by+c=0\) is given by the formula:
\(D=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
- When the line is horizontal the formula transforms to: \(D=|P_y-L_y|\)
Where: \(P_y\) is the y-coordinate of the given point P; \(L_y\) is the y-coordinate of any point on the given vertical line L. | | the vertical bars mean "absolute value" - make it positive even if it calculates to a negative. - When the line is vertical the formula transforms to: \(D=|P_x-L_x|\)
Where: \(P_x\) is the x-coordinate of the given point P; \(L_x\) is the x-coordinate of any point on the given vertical line L. | | the vertical bars mean "absolute value" - make it positive even if it calculates to a negative. - When the given point is origin, then the distance between origin and line ax+by+c=0 is given by the formula:
\(D=\frac{|c|}{\sqrt{a^2+b^2}}\)
Re: GRE Quant - Coordinate Geometry Lines Theory
[#permalink]
 11 Jul 2020, 11:14
11 Jul 2020, 11:14
Expert Reply
Coordinate Geometry Lines Questions by Tag
Quantitative Comparison Questions
Multiple-choice Questions — Select One Answer Choice
Multiple-choice Questions — Select One or More Answer Choices
Numeric Entry Question
Data Interpretation Sets
HARD QuestionsMEDIUM QuestionsEASY Questions
Re: GRE Quant - Coordinate Geometry Lines Theory
[#permalink]
 19 Jul 2020, 10:02
19 Jul 2020, 10:02
Expert Reply
1) GRE Lesson: Graphing lines


