
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If |x - 5| + |x - 7| < 4, what is the range of values of x ? (A) 4 <
[#permalink]
 15 Nov 2021, 03:13
15 Nov 2021, 03:13
Expert Reply
1
Bookmarks
Question Stats:
 88% (01:31) correct
88% (01:31) correct
 11% (02:08) wrong
11% (02:08) wrong  based on 17 sessions
based on 17 sessions
Hide Show timer Statistics
If |x - 5| + |x - 7| < 4, what is the range of values of x ?
(A) 4 < x < 8
(B) -4 < x < 8
(C) 3 < x < 5
(D) -8 < x < -4
(E) -4 < x < 4
(A) 4 < x < 8
(B) -4 < x < 8
(C) 3 < x < 5
(D) -8 < x < -4
(E) -4 < x < 4
Moderator

Joined: 02 Jan 2020
Status:GRE Quant Tutor
Posts: 1141
Given Kudos: 9
Location: India
Concentration: General Management
Schools: XLRI Jamshedpur, India - Class of 2014
GMAT 1: 700 Q51 V31
GPA: 2.8
WE:Engineering (Computer Software)
If |x - 5| + |x - 7| < 4, what is the range of values of x ? (A) 4 <
[#permalink]
 30 Dec 2021, 22:12
30 Dec 2021, 22:12
1
Given that |x - 5| + |x - 7| < 4 and we need to find the range of values of x
Let's solve the problem using three methods
Method 1: Substitution
Let's take values in each answer choice and substitutive in the equation and check which one satisfies the equation.
If you glance through the answer choices then you will see that if u take x=0 and are able to prove it wrong then we can eliminate B and E
(B), (E) : x=0
=> |x - 5| + |x - 7| < 4 => |0 - 5| + |0 - 7| < 4 => 5 + 7 = 12 NOT LESS THAN 4
=> FALSE
(A) 4 < x < 8 x = 7
=> |7 - 5| + |7 - 7| < 4 => |2| + 0 < 4
=> TRUE => Possible
(C) 3 < x < 5 x = 4
=> |4 - 5| + |4 - 7| < 4 => |-1| + |-3| = 4 NOT LESS THAN 4
=> FALSE
(D) -8 < x < -4 x = -5
=> |-5 - 5| + |-5 - 7| < 4 => |-10| + |-12| < 4 => 10 + 12 NOT LESS THAN 4
=> FALSE
Method 2: Algebra
|x - 5| + |x - 7| < 4
Let's find the points where the values inside the Absolute Value will change signs
=> x-5 = 0 => x = 5
=> x-7 = 0 => x = 7
So, we can divide the number line into three parts
x < 5, 5 <= x < 7 , x > 7
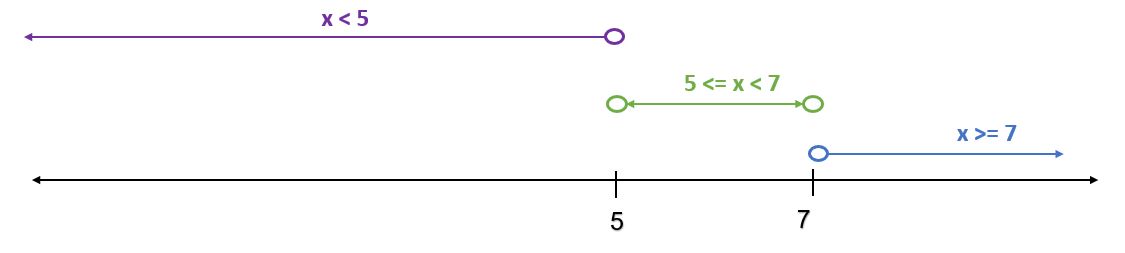
5 to 7.JPG [ 19.92 KiB | Viewed 2467 times ]
Case 1: x < 5
|x - 5| = -(x-5) (as x-5 will be negative)
|x - 7| = -(x-7) (as x-7 will be negative)
=> -(x - 5) + (-(x - 7)) < 4 => -x + 5 -x +7 < 4 => -2x + 12 < 4
=> -2x < 4-12 => -2x < -8 => x > \(\frac{-8}{-2}\) => x > 4
But the condition was x < 5
So, intersection is 4 < x < 5
Case 2: 5 <= x < 7
|x - 5| = x-5 (as x-5 will be non-negative)
|x - 7| = -(x-7) (as x-7 will be negative)
=> x - 5 + (-(x - 7)) < 4 => x - 5 -x +7 < 4 => 2 < 4
Which is always true
=> 5 <= x < 7
Case 3: x >= 7
|x - 5| = x-5 (as x-5 will be non-negative)
|x - 7| = x-7 (as x-7 will be non-negative)
=> x - 5 + x - 7 < 4 => -x + 5 + x -7 < 4 => 2x - 12 < 4
=> 2x < 4+12 => 2x < 16 => x < \(\frac{16}{2}\) => x < 8
But the condition was x >= 7
So, intersection is 7 <= x < 8
So, solution is 4 < x < 5, 5 <= x < 7, 7 <= x < 8
Which is nothing but 4 < x < 8
Method 3: Graphical Method
| x - 5 | is the distance between x and 5
| x - 7 | is the distance between x and 7
Case 1: If we take a value of x between 5 and 7

between 5 and 7.JPG [ 15.76 KiB | Viewed 2460 times ]
Then, the distance between x and 5 + Distance between x and 7 = Distance between 5 and 7 = 2 < 4
=> All values between 5 and 7 inclusive are possible
Case 2: If we take a value of x < 5
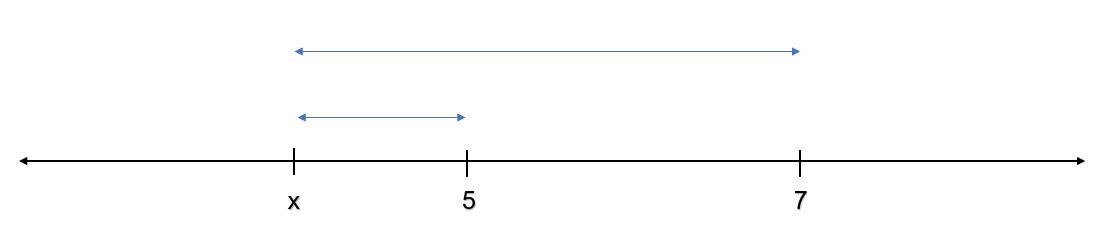
x lt 5.JPG [ 17.1 KiB | Viewed 2467 times ]
Then Distance between x and 7 = Distance between x and 5 + Distance between 5 and 7
=> Distance between x and 7 = Distance between x and 5 + 2
So, for Distance between x and 5 + Distance between x and 7 < 4
=> Distance between x and 5 + Distance between x and 5 + 2 < 4
=> 2 * Distance between x and 5 < 4-2
=> Distance between x and 5 < 1
So, If x is at a distance of less than 1 from 5 on the left hand side then it is possible
=> 4 < x <= 5
Case 3: If we take a value of x > 7
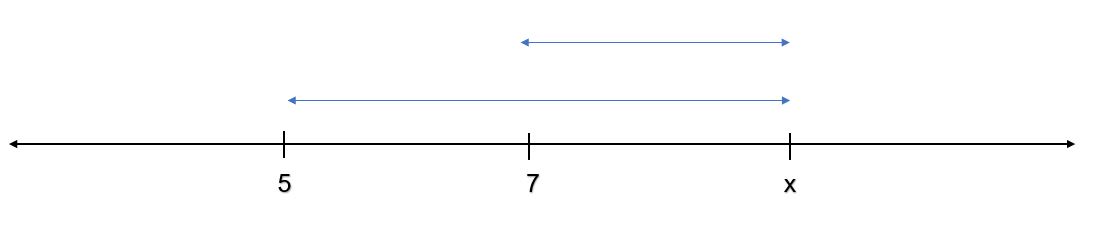
x gt 7.JPG [ 19.27 KiB | Viewed 2461 times ]
Then Distance between x and 5 = Distance between x and 7 + Distance between 5 and 7
=> Distance between x and 5 = Distance between x and 7 + 2
So, for Distance between x and 5 + Distance between x and 7 < 4
=> Distance between x and 7 + 2 + Distance between x and 7 < 4
=> 2 * Distance between x and 7 < 4-2
=> Distance between x and 7 < 1
So, If x is at a distance of less than 1 from 7 on the right hand side then it is possible
=> 7 =< x < 8
So, solution is 4 < x < 5, 5 <= x < 7, 7 <= x < 8
Which is nothing but 4 < x < 8
So, Answer will be A
Hope it helps!
Watch the following video to learn How to Solve Absolute Value Problems
Let's solve the problem using three methods
Method 1: Substitution
Let's take values in each answer choice and substitutive in the equation and check which one satisfies the equation.
If you glance through the answer choices then you will see that if u take x=0 and are able to prove it wrong then we can eliminate B and E
(B), (E) : x=0
=> |x - 5| + |x - 7| < 4 => |0 - 5| + |0 - 7| < 4 => 5 + 7 = 12 NOT LESS THAN 4
=> FALSE
(A) 4 < x < 8 x = 7
=> |7 - 5| + |7 - 7| < 4 => |2| + 0 < 4
=> TRUE => Possible
(C) 3 < x < 5 x = 4
=> |4 - 5| + |4 - 7| < 4 => |-1| + |-3| = 4 NOT LESS THAN 4
=> FALSE
(D) -8 < x < -4 x = -5
=> |-5 - 5| + |-5 - 7| < 4 => |-10| + |-12| < 4 => 10 + 12 NOT LESS THAN 4
=> FALSE
Method 2: Algebra
|x - 5| + |x - 7| < 4
Let's find the points where the values inside the Absolute Value will change signs
=> x-5 = 0 => x = 5
=> x-7 = 0 => x = 7
So, we can divide the number line into three parts
x < 5, 5 <= x < 7 , x > 7
Attachment:
5 to 7.JPG [ 19.92 KiB | Viewed 2467 times ]
Case 1: x < 5
|x - 5| = -(x-5) (as x-5 will be negative)
|x - 7| = -(x-7) (as x-7 will be negative)
=> -(x - 5) + (-(x - 7)) < 4 => -x + 5 -x +7 < 4 => -2x + 12 < 4
=> -2x < 4-12 => -2x < -8 => x > \(\frac{-8}{-2}\) => x > 4
But the condition was x < 5
So, intersection is 4 < x < 5
Case 2: 5 <= x < 7
|x - 5| = x-5 (as x-5 will be non-negative)
|x - 7| = -(x-7) (as x-7 will be negative)
=> x - 5 + (-(x - 7)) < 4 => x - 5 -x +7 < 4 => 2 < 4
Which is always true
=> 5 <= x < 7
Case 3: x >= 7
|x - 5| = x-5 (as x-5 will be non-negative)
|x - 7| = x-7 (as x-7 will be non-negative)
=> x - 5 + x - 7 < 4 => -x + 5 + x -7 < 4 => 2x - 12 < 4
=> 2x < 4+12 => 2x < 16 => x < \(\frac{16}{2}\) => x < 8
But the condition was x >= 7
So, intersection is 7 <= x < 8
So, solution is 4 < x < 5, 5 <= x < 7, 7 <= x < 8
Which is nothing but 4 < x < 8
Method 3: Graphical Method
| x - 5 | is the distance between x and 5
| x - 7 | is the distance between x and 7
Case 1: If we take a value of x between 5 and 7
Attachment:
between 5 and 7.JPG [ 15.76 KiB | Viewed 2460 times ]
Then, the distance between x and 5 + Distance between x and 7 = Distance between 5 and 7 = 2 < 4
=> All values between 5 and 7 inclusive are possible
Case 2: If we take a value of x < 5
Attachment:
x lt 5.JPG [ 17.1 KiB | Viewed 2467 times ]
Then Distance between x and 7 = Distance between x and 5 + Distance between 5 and 7
=> Distance between x and 7 = Distance between x and 5 + 2
So, for Distance between x and 5 + Distance between x and 7 < 4
=> Distance between x and 5 + Distance between x and 5 + 2 < 4
=> 2 * Distance between x and 5 < 4-2
=> Distance between x and 5 < 1
So, If x is at a distance of less than 1 from 5 on the left hand side then it is possible
=> 4 < x <= 5
Case 3: If we take a value of x > 7
Attachment:
x gt 7.JPG [ 19.27 KiB | Viewed 2461 times ]
Then Distance between x and 5 = Distance between x and 7 + Distance between 5 and 7
=> Distance between x and 5 = Distance between x and 7 + 2
So, for Distance between x and 5 + Distance between x and 7 < 4
=> Distance between x and 7 + 2 + Distance between x and 7 < 4
=> 2 * Distance between x and 7 < 4-2
=> Distance between x and 7 < 1
So, If x is at a distance of less than 1 from 7 on the right hand side then it is possible
=> 7 =< x < 8
So, solution is 4 < x < 5, 5 <= x < 7, 7 <= x < 8
Which is nothing but 4 < x < 8
So, Answer will be A
Hope it helps!
Watch the following video to learn How to Solve Absolute Value Problems
General Discussion
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: If |x - 5| + |x - 7| < 4, what is the range of values of x ? (A) 4 <
[#permalink]
 15 Nov 2021, 06:25
15 Nov 2021, 06:25
1
Carcass wrote:
If |x - 5| + |x - 7| < 4, what is the range of values of x ?
(A) 4 < x < 8
(B) -4 < x < 8
(C) 3 < x < 5
(D) -8 < x < -4
(E) -4 < x < 4
(A) 4 < x < 8
(B) -4 < x < 8
(C) 3 < x < 5
(D) -8 < x < -4
(E) -4 < x < 4
For these kinds of questions, I typically find that the easiest/fastest approach is to simply test numbers.
For example, is x = 0 a solution to |x - 5| + |x - 7| < 4?
Plug x = 0 into the inequality to get: |0 - 5| + |0 - 7| < 4
Simplify: 5 + 7 < 4. Doesn't work!
So x = 0 is NOT a solution, which means we can eliminate B and E, since they say that x = 0 IS a solution.
Now let's test x = 4
Plug x = 4 into the inequality to get: |4 - 5| + |4 - 7| < 4
Simplify: 1 + 3 < 4. Doesn't work!
Since x = 4 is NOT a solution, we can eliminate C, since it says x = 4 IS a solution.
We're down to A and D.
We'll test x = 6 to get: |6 - 5| + |6 - 7| < 4
Simplify: 1 + 1 < 4. WORKS!
Since x = 6 is a solution, we can eliminate D, since it says x = 6 is NOT a solution.
Answer: A





