GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If a can range from 45° to 60°, which of the following are possible va
[#permalink]
08 Dec 2022, 14:24
08 Dec 2022, 14:24
Expert Reply
1
Bookmarks
00:00
Question Stats:
54% (01:39) correct
45% (02:22) wrong based on 11 sessions
Hide Show timer Statistics
Attachment:
GRE If a can range from 45° to 60.jpg [ 11.56 KiB | Viewed 1488 times ]
If a can range from 45° to 60°, which of the following are possible values for y ?
Indicate all such values.
2
3
4
5
6
7
8
Re: If a can range from 45° to 60°, which of the following are possible va
[#permalink]
08 Dec 2022, 18:56
08 Dec 2022, 18:56
explanation?
If a can range from 45° to 60°, which of the following are possible va
[#permalink]
10 Dec 2022, 12:27
10 Dec 2022, 12:27
Since angle a has a minimum of 45 degrees and a maximum of 60 degrees, then the y coordinate will a range of values between the minimum and maximum angles.
Let's fine the minimum first:
45 degrees.jpg [ 17.88 KiB | Viewed 1456 times ]
If angle a = 45 degrees, then we have special 45-45-90 isosceles triangle with sides 4-4-4 sq root 2. That means in this case y = 4
Now for the maximum:
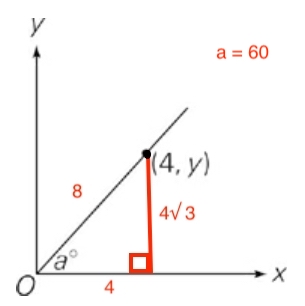
60 degrees.jpg [ 18.73 KiB | Viewed 1423 times ]
If angle a = 60 degrees, then we have another special triangle, a 30-60-90 triangle. This has the unique properties of having a side length ratio of (small leg) : (larger leg) : (hypotenuse) = x : x square root 3: 2x.
That means y = 4 square root 3 which is approximately equal to 6.9
So now that we have the minimum and maximum values for y, we can set up an inequality:
4 ≤ y ≤ 6.9 -----> Answer Choices C , D and E
Hope this helps!
Let's fine the minimum first:
Attachment:
45 degrees.jpg [ 17.88 KiB | Viewed 1456 times ]
If angle a = 45 degrees, then we have special 45-45-90 isosceles triangle with sides 4-4-4 sq root 2. That means in this case y = 4
Now for the maximum:
Attachment:
60 degrees.jpg [ 18.73 KiB | Viewed 1423 times ]
If angle a = 60 degrees, then we have another special triangle, a 30-60-90 triangle. This has the unique properties of having a side length ratio of (small leg) : (larger leg) : (hypotenuse) = x : x square root 3: 2x.
That means y = 4 square root 3 which is approximately equal to 6.9
So now that we have the minimum and maximum values for y, we can set up an inequality:
4 ≤ y ≤ 6.9 -----> Answer Choices C , D and E
Hope this helps!
