
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
One ounce of Solution X contains only ingredients a and b in a ratio o
[#permalink]
 01 Jun 2023, 05:07
01 Jun 2023, 05:07
Expert Reply
3
Bookmarks
Question Stats:
 75% (02:32) correct
75% (02:32) correct
 24% (02:49) wrong
24% (02:49) wrong  based on 29 sessions
based on 29 sessions
Hide Show timer Statistics
One ounce of Solution X contains only ingredients a and b in a ratio of 2 : 3. One ounce of Solution Y contains only ingredients a and b in a ratio of 1 : 2. If Solution Z is created by mixing solutions X and Y in a ratio of 3 : 11, then 630 ounces of Solution Z contains how many ounces of a ?
A. 68
B. 73
C, 89
D. 219
E. 236
Post A Detailed Correct Solution For The Above Questions And Get A Kudos.
Question From Our Project: Free GRE Prep Club Tests in Exchange for 20 Kudos
\(\Longrightarrow\) Cracking the GRE Premium
\(\Longrightarrow\) GRE Math Essentials - A most comprehensive handout!!
A. 68
B. 73
C, 89
D. 219
E. 236
Post A Detailed Correct Solution For The Above Questions And Get A Kudos.
Question From Our Project: Free GRE Prep Club Tests in Exchange for 20 Kudos
\(\Longrightarrow\) Cracking the GRE Premium
\(\Longrightarrow\) GRE Math Essentials - A most comprehensive handout!!
Re: One ounce of Solution X contains only ingredients a and b in a ratio o
[#permalink]
 01 Jun 2023, 17:32
01 Jun 2023, 17:32
1
X = 3/14 * 630
Y = 11/14 * 630
a = 2/5 * 3/14 * 630 + 1/3 * 11/14 * 630 = 45(6/5 + 11/3) = 54 + 165 = 219
Option D
Y = 11/14 * 630
a = 2/5 * 3/14 * 630 + 1/3 * 11/14 * 630 = 45(6/5 + 11/3) = 54 + 165 = 219
Option D
Re: One ounce of Solution X contains only ingredients a and b in a ratio o
[#permalink]
 03 Jun 2023, 04:00
03 Jun 2023, 04:00
1
Expert Reply
OE
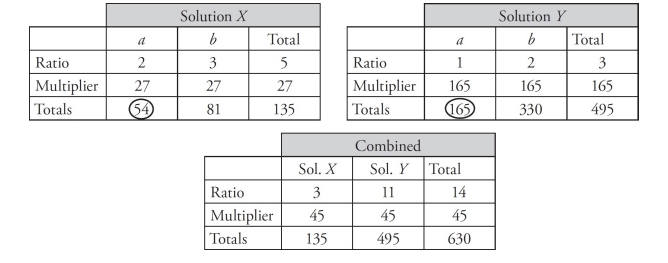
This is a question about ratios, so draw ratio boxes for each ratio. The question states that one ounce of Solution X contains ingredients a and b in the ratio of 2:3, which means that for every 2 parts of a there are 3 parts of b. That makes 5 parts in total. So, enter 2, 3 and 5 in the top row of a ratio box marked Solution X. One ounce of Solution Y contains ingredients a and b in the ratio of 1:2, which means that for every 1 part of a there are 2 parts of b. That makes 3 parts in total. So, enter 1, 2, and 3 in the top row of a ratio box marked Solution Y.
The combined solution of 630 ounces contains Solution X and Solution Y in the ratio of 3:11, which means that for every 3 ounces of Solution X there are 11 ounces of Solution Y. That makes 14 ounces in total. So, enter 3, 11, and 14 in the top row of a ratio box marked Combined, and enter 630 in the last row under the Total column in the Combined ratio box. Divide 630 by 14 to get 45 as the multiplier in the Combined ratio box. Multiply 45 times 3 to get 135 ounces of Solution X, and multiply 45 times 11 to get 495 ounces of Solution Y. Enter 135 in the last row under the Total column in the Solution X ratio box and enter 495 in the last row under the Total column in the Solution Y ratio box.
Now divide 135 by 5 to get 27 as the multiplier in the Solution X ratio box and divide 495 by 3 to get 165 as the multiplier in the Solution Y ratio box. The question asks how many ounces of ingredient a are in the combined solution. Multiply 27 times 2 to get 54 ounces of ingredient a from Solution X and multiply 165 times 1 to get 165 ounces of ingredient a from Solution Y. Add 54 plus 165 to get 219 ounces of ingredient a. The correct answer is (D).
GRE mixture (2).jpg [ 66.05 KiB | Viewed 3768 times ]
This is a question about ratios, so draw ratio boxes for each ratio. The question states that one ounce of Solution X contains ingredients a and b in the ratio of 2:3, which means that for every 2 parts of a there are 3 parts of b. That makes 5 parts in total. So, enter 2, 3 and 5 in the top row of a ratio box marked Solution X. One ounce of Solution Y contains ingredients a and b in the ratio of 1:2, which means that for every 1 part of a there are 2 parts of b. That makes 3 parts in total. So, enter 1, 2, and 3 in the top row of a ratio box marked Solution Y.
The combined solution of 630 ounces contains Solution X and Solution Y in the ratio of 3:11, which means that for every 3 ounces of Solution X there are 11 ounces of Solution Y. That makes 14 ounces in total. So, enter 3, 11, and 14 in the top row of a ratio box marked Combined, and enter 630 in the last row under the Total column in the Combined ratio box. Divide 630 by 14 to get 45 as the multiplier in the Combined ratio box. Multiply 45 times 3 to get 135 ounces of Solution X, and multiply 45 times 11 to get 495 ounces of Solution Y. Enter 135 in the last row under the Total column in the Solution X ratio box and enter 495 in the last row under the Total column in the Solution Y ratio box.
Now divide 135 by 5 to get 27 as the multiplier in the Solution X ratio box and divide 495 by 3 to get 165 as the multiplier in the Solution Y ratio box. The question asks how many ounces of ingredient a are in the combined solution. Multiply 27 times 2 to get 54 ounces of ingredient a from Solution X and multiply 165 times 1 to get 165 ounces of ingredient a from Solution Y. Add 54 plus 165 to get 219 ounces of ingredient a. The correct answer is (D).
Attachment:
GRE mixture (2).jpg [ 66.05 KiB | Viewed 3768 times ]






