
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Each of the arcs are quarter circles. Find the area of the shaded regi
[#permalink]
 28 Mar 2024, 01:31
28 Mar 2024, 01:31
Expert Reply
2
Bookmarks
Question Stats:
 72% (02:15) correct
72% (02:15) correct
 27% (01:06) wrong
27% (01:06) wrong  based on 11 sessions
based on 11 sessions
Hide Show timer Statistics
Attachment:
GRE Each of the arcs.jpg [ 31.8 KiB | Viewed 1619 times ]
Each of the arcs are quarter circles. Find the area of the shaded region.
A. \(4 \pi -8 \)
B. \(\frac{25\pi}{4} -\frac{25}{2}\)
C. \(8 \pi-16\)
D. \(25-\frac{25 \pi }{4}\)
E. \(13\)
Part of the project: The Butler-GRE Daily New Quant and Verbal Questions to Practice (2023) - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
Manager

Joined: 11 Nov 2023
Posts: 228
Given Kudos: 78
WE:Business Development (Advertising and PR)
Each of the arcs are quarter circles. Find the area of the shaded regi
[#permalink]
 10 May 2024, 10:43
10 May 2024, 10:43
2
The key here is that the area of each "leaf" is the area of the quarter circle minus the area of the triangle defined by the secant and radii. In the illustration, I added labels A-E to points on the circles.
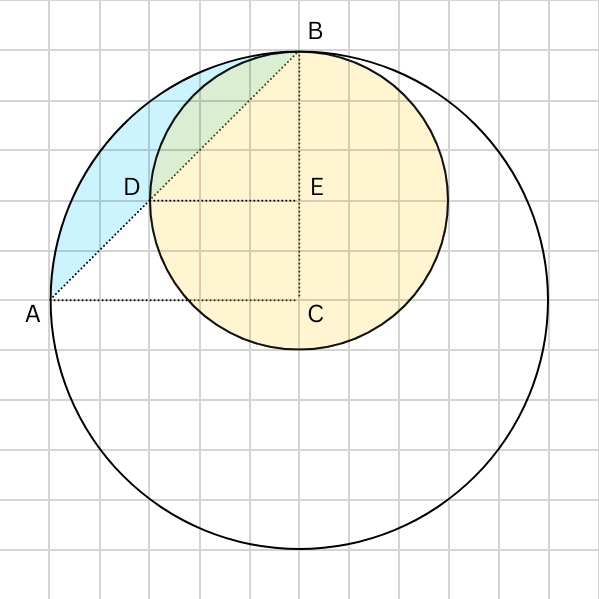
overlapping_arcs.png [ 48.4 KiB | Viewed 1403 times ]
First, let's find the area of the bigger leaf. The circle's center is C with a radius of 5. Thus, the area of the quarter circle is \(\frac{25\pi}{4}\).
Sides AC and BC are radii, so they are both 5. The area of triangle ABC is \(\frac{25}{2}\).
To isolate just the shaded arc's area, we subtract the area of the right triangle ABC. That gets us the area of half of the bigger leaf, \(\frac{25\pi}{4} - \frac{25}{2}\)
Now we double that to get the area of the full leaf, \(\frac{25\pi}{2} - 25\).
Now, we can do the same process to find the area of the smaller leaf. The circle's center is E with a radius of 3, and the area of quarter circle is \(\frac{9\pi}{4}\). The area of triangle DBE is \(\frac{9}{2}\).
The area of the smaller leaf is \(\frac{9\pi}{2} -9\).
Finally, we subtract the area of the smaller leaf from the bigger leaf to find the area of the shaded region.
\((\frac{25\pi}{2} - 25) - (\frac{9\pi}{2} -9) = 8 \pi-16\)
Attachment:
overlapping_arcs.png [ 48.4 KiB | Viewed 1403 times ]
First, let's find the area of the bigger leaf. The circle's center is C with a radius of 5. Thus, the area of the quarter circle is \(\frac{25\pi}{4}\).
Sides AC and BC are radii, so they are both 5. The area of triangle ABC is \(\frac{25}{2}\).
To isolate just the shaded arc's area, we subtract the area of the right triangle ABC. That gets us the area of half of the bigger leaf, \(\frac{25\pi}{4} - \frac{25}{2}\)
Now we double that to get the area of the full leaf, \(\frac{25\pi}{2} - 25\).
Now, we can do the same process to find the area of the smaller leaf. The circle's center is E with a radius of 3, and the area of quarter circle is \(\frac{9\pi}{4}\). The area of triangle DBE is \(\frac{9}{2}\).
The area of the smaller leaf is \(\frac{9\pi}{2} -9\).
Finally, we subtract the area of the smaller leaf from the bigger leaf to find the area of the shaded region.
\((\frac{25\pi}{2} - 25) - (\frac{9\pi}{2} -9) = 8 \pi-16\)
General Discussion
Re: Each of the arcs are quarter circles. Find the area of the shaded regi
[#permalink]
 10 May 2024, 15:24
10 May 2024, 15:24
Expert Reply
beautiful explanation. Even by graph




