
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A point R has coordinates (a, b)
[#permalink]
 Updated on: 25 Nov 2025, 08:57
Updated on: 25 Nov 2025, 08:57
2
Expert Reply
2
Bookmarks
Question Stats:
 68% (02:11) correct
68% (02:11) correct
 31% (01:44) wrong
31% (01:44) wrong  based on 16 sessions
based on 16 sessions
Hide Show timer Statistics
A point R has coordinates (a, b) whereas point S has coordinates (m, n). If a < 0, and b, m, n > 0, and b > m, then for the line \(l_{1}\) connecting two points R and S:
A. Quantity A is greater.
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.
Quantity A |
Quantity B |
Slope of \(l_{1}\) |
0 |
A. Quantity A is greater.
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.
Re: A point R has coordinates (a, b)
[#permalink]
 05 Dec 2021, 02:35
05 Dec 2021, 02:35
1
Expert Reply
1
Bookmarks
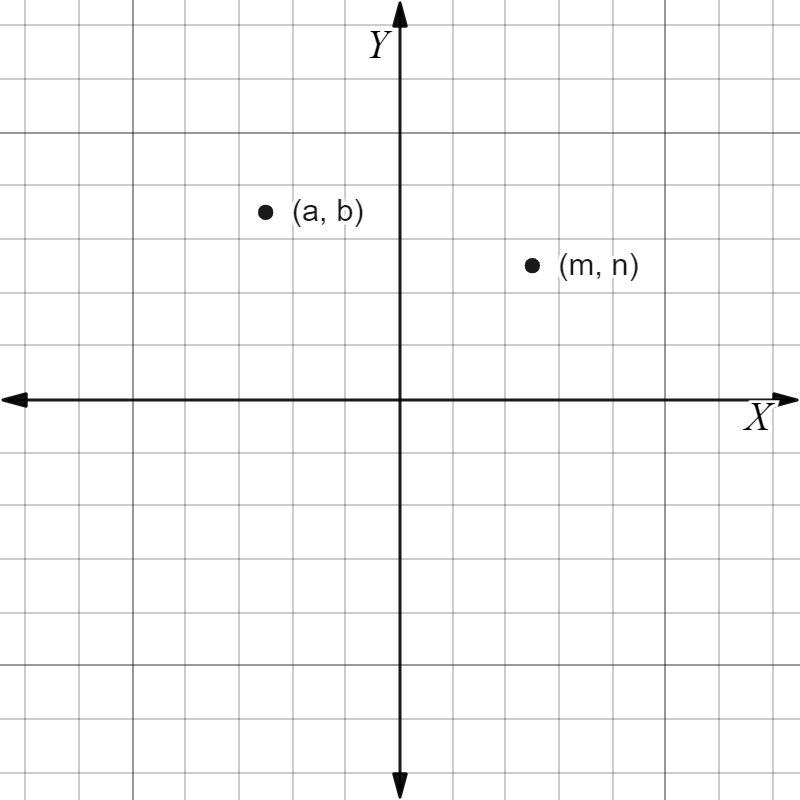
Since, the x-coordinate a of point R is less than 0 and the y-coordinate b of point R is greater than 0, it means the point R lies in the 2nd quadrant where the x-axis is negative and y-axis is positive.
x-coordinate of point R < 0 implies a < 0
y-coordinate of point R > 0 implies b > 0
Similarly, x-coordinate m and y-coordinate n of the point S are greater than 0, it means the point R lies in the 1st quadrant where both axis are positive.
x-coordinate of point S > 0 implies m > 0
y-coordinate of point S > 0 implies n > 0
However, we are also told that the y-coordinate b of the point R is greater than the y-coordinate n of the point S.
y-coordinate of point R > y-coordinate of point S
a > m
After understanding the placement of both points $R$ and $S$, we can say that the line will go downwards because the point R will be placed higher in the 2nd quadrant as compared to the point S in the 1st quadrant. Therefore, the slope of the line \(\bar{RS}\) will be negative.
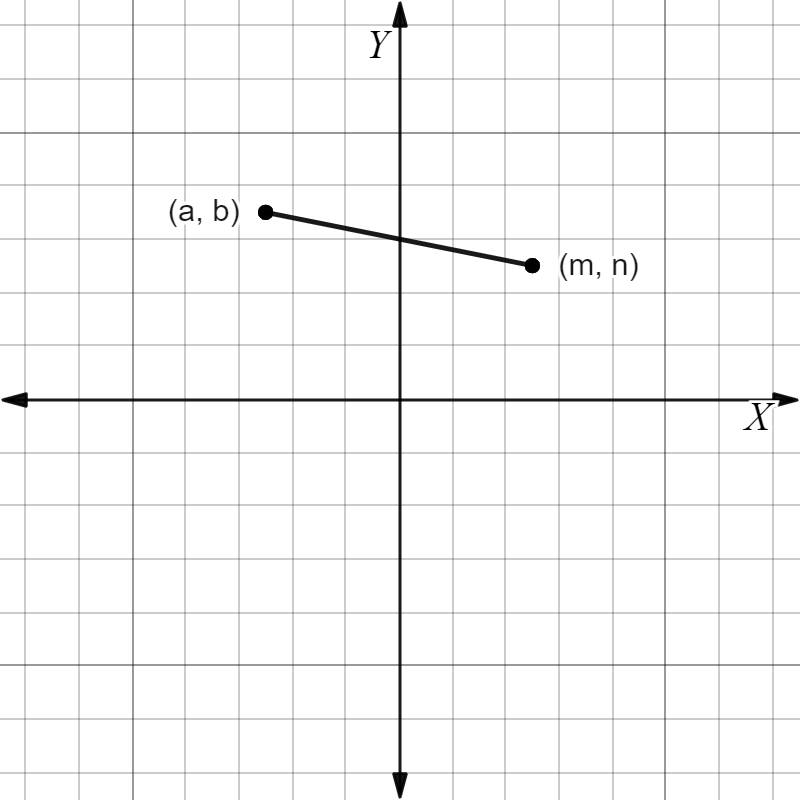
Quantity A = Slope of \(l_{1}\), which is negative
Quantity B = 0
Quantity A < Quantity B
Hence, the correct answer is Option B).
x-coordinate of point R < 0 implies a < 0
y-coordinate of point R > 0 implies b > 0
Similarly, x-coordinate m and y-coordinate n of the point S are greater than 0, it means the point R lies in the 1st quadrant where both axis are positive.
x-coordinate of point S > 0 implies m > 0
y-coordinate of point S > 0 implies n > 0
However, we are also told that the y-coordinate b of the point R is greater than the y-coordinate n of the point S.
y-coordinate of point R > y-coordinate of point S
a > m

After understanding the placement of both points $R$ and $S$, we can say that the line will go downwards because the point R will be placed higher in the 2nd quadrant as compared to the point S in the 1st quadrant. Therefore, the slope of the line \(\bar{RS}\) will be negative.

Quantity A = Slope of \(l_{1}\), which is negative
Quantity B = 0
Quantity A < Quantity B
Hence, the correct answer is Option B).






