GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
The random variable x has the following continuous probabil
[#permalink]
26 Aug 2017, 01:55
26 Aug 2017, 01:55
1
Expert Reply
25
Bookmarks
00:00
Question Stats:
26% (02:31) correct
73% (02:00) wrong based on 145 sessions
Hide Show timer Statistics
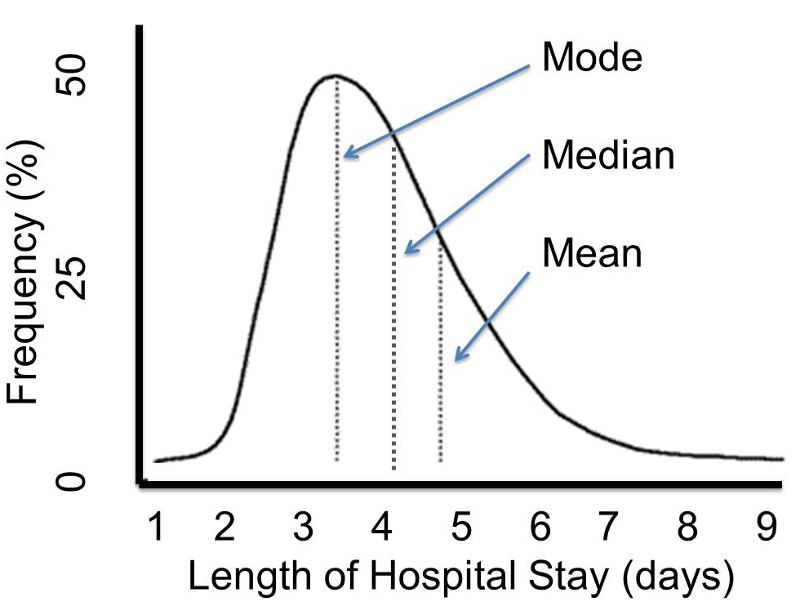
The random variable x has the following continuous probability distribution in the range 0 ≤ x ≤ \(\sqrt{2}\), as shown in the coordinate plane with x on the horizontal axis:
The probability that x < 0 = the probability that \(x > \sqrt{2} = 0\).
What is the median of x?
A. \(\frac{\sqrt{2} - 1}{2}\)
B. \(\frac{\sqrt{2}}{4}\)
C. \(\sqrt{2}^{-1}\)
D. \(\frac{\sqrt{2} + 1}{4}\)
E. \(\frac{\sqrt{2}}{2}\)
The random variable x has the following continuous probabil
[#permalink]
03 Mar 2018, 04:34
03 Mar 2018, 04:34
13
Expert Reply
A median value of any probability distribution divides the area under the probabaility distribution in two equal parts.
Best understood with following image.
Now in our case we need to split the triangular distribution along a line \(x=?\) (parallel to y axis) such that area of the right half is same as the left half.
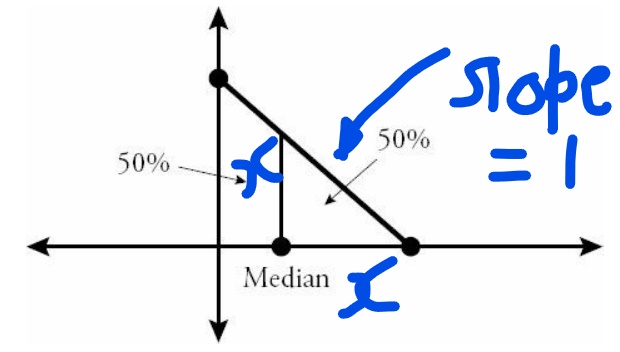
Area of right half = \(\frac{1}{2} \times\) Area of the larger triangle.
Now look at the figure below and we have marked out the hight and length of the triangle as x. Now height = length for this triangle because the given line has slope 1.
Area of right half = \(\frac{1}{2} \times x^2\)= \(\frac{1}{2} \times \frac{1}{2}\times \sqrt{2}^2\).
Solving for x we get x =1. So median value has to be \(\sqrt{2}-1\) (refer to the figure above)
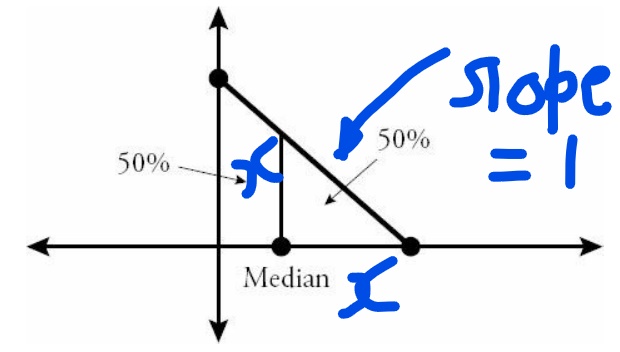
Inkedtriangle_LI.jpg [ 841.95 KiB | Viewed 15698 times ]
Skewed.png [ 131.58 KiB | Viewed 15696 times ]
Best understood with following image.
Now in our case we need to split the triangular distribution along a line \(x=?\) (parallel to y axis) such that area of the right half is same as the left half.
Area of right half = \(\frac{1}{2} \times\) Area of the larger triangle.
Now look at the figure below and we have marked out the hight and length of the triangle as x. Now height = length for this triangle because the given line has slope 1.
Area of right half = \(\frac{1}{2} \times x^2\)= \(\frac{1}{2} \times \frac{1}{2}\times \sqrt{2}^2\).
Solving for x we get x =1. So median value has to be \(\sqrt{2}-1\) (refer to the figure above)
Show: ::
Attachment:
Inkedtriangle_LI.jpg [ 841.95 KiB | Viewed 15698 times ]
Attachment:
Skewed.png [ 131.58 KiB | Viewed 15696 times ]
Re: The random variable x has the following continuous probabil
[#permalink]
18 Sep 2017, 02:25
18 Sep 2017, 02:25
6
1
Bookmarks
Carcass wrote:
The random variable x has the following continuous probability distribution in the range 0 ≤ x ≤ \(\sqrt{2}\), as shown in the coordinate plane with x on the horizontal axis:
The probability that x < 0 = the probability that \(x > \sqrt{2} = 0\).
What is the median of x?
A. \(\frac{\sqrt{2} - 1}{2}\)
B. \(\frac{\sqrt{2}}{4}\)
C. \(\sqrt{2}^{-1}\)
D. \(\frac{\sqrt{2} + 1}{4}\)
E. \(\frac{\sqrt{2}}{2}\)
The probability that x < 0 = the probability that \(x > \sqrt{2} = 0\).
What is the median of x?
A. \(\frac{\sqrt{2} - 1}{2}\)
B. \(\frac{\sqrt{2}}{4}\)
C. \(\sqrt{2}^{-1}\)
D. \(\frac{\sqrt{2} + 1}{4}\)
E. \(\frac{\sqrt{2}}{2}\)
\(\sqrt{2}^{-1}\) and \(\frac{\sqrt{2}}{2}\) are the same expression. One is the rationalized form of the other. Thus they should be both right.
