
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Natural Resource Industries' Output as a Percentage of Gr
[#permalink]
 21 Oct 2017, 04:40
21 Oct 2017, 04:40
Expert Reply
10
Bookmarks
Question Stats:
 73% (05:24) correct
73% (05:24) correct
 26% (05:44) wrong
26% (05:44) wrong  based on 34 sessions
based on 34 sessions
Hide Show timer Statistics
Natural Resource Industries' Output as a Percentage of Gross Domestic Product in Province P 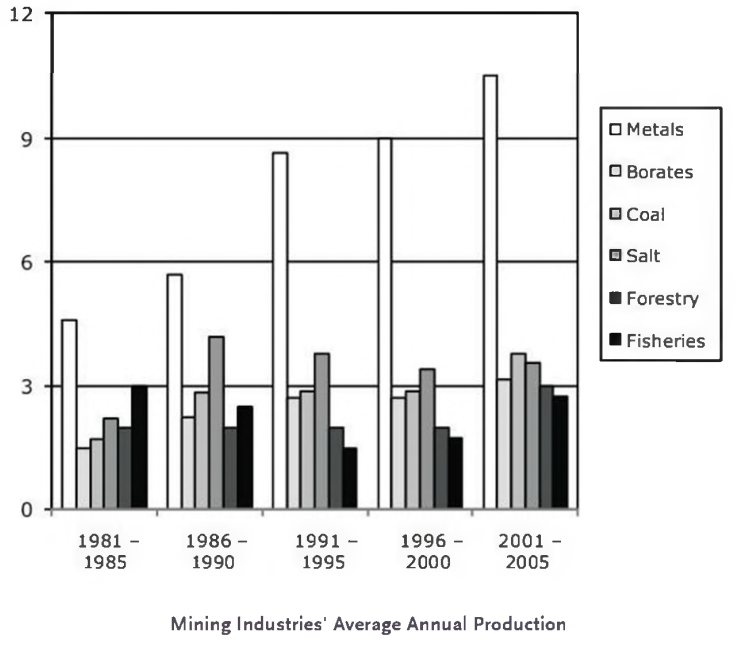
#GREpracticequestion Approximately what percent of the mining industries’.jpg [ 107.54 KiB | Viewed 12333 times ]
Mining Industries' Average Annual Production 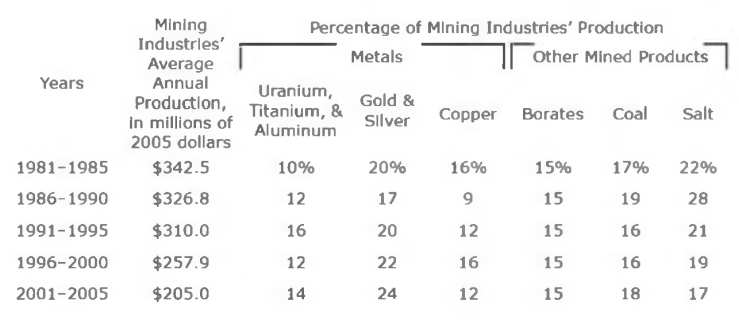
#GREpracticequestion Approximately what percent of average annual GDP .jpg [ 79.29 KiB | Viewed 12338 times ]
Attachment:
#GREpracticequestion Approximately what percent of the mining industries’.jpg [ 107.54 KiB | Viewed 12333 times ]
Attachment:
#GREpracticequestion Approximately what percent of average annual GDP .jpg [ 79.29 KiB | Viewed 12338 times ]
Approximately what percent of the mining industries’ average annual production from 1991-1995 came from production of aluminum?
(A) 4 %
(B) 7 %
(C) 11%
(D) 22 %
(E) Cannot be determined
Approximately what percent of average annual GDP of Province P from 1996-2000 came from copper production?
(A) 3 %
(B) 6 %
(C) 9 %
(D) 14 %
(E) 18%
Which of the following statements can be inferred from the information given?
□ For all the time periods shown, borate production, in millions of 2005dollars, was the same.
□ Of the time periods shown, 1981-1985 was the one in which the mining industries produced the greatest value of gold and silver, measured in 2005 dollars.
□ Of the time periods shown, 2001-2005 had the highest average annual GDP, measured in 2005 dollars.
(A) 4 %
(B) 7 %
(C) 11%
(D) 22 %
(E) Cannot be determined
Show: :: OA
E
Approximately what percent of average annual GDP of Province P from 1996-2000 came from copper production?
(A) 3 %
(B) 6 %
(C) 9 %
(D) 14 %
(E) 18%
Show: :: OA
A
Which of the following statements can be inferred from the information given?
□ For all the time periods shown, borate production, in millions of 2005dollars, was the same.
□ Of the time periods shown, 1981-1985 was the one in which the mining industries produced the greatest value of gold and silver, measured in 2005 dollars.
□ Of the time periods shown, 2001-2005 had the highest average annual GDP, measured in 2005 dollars.
Show: :: OA
II only
Sherpa Prep Representative
Joined: 15 Jan 2018
Posts: 147
Given Kudos: 0
Re: Natural Resource Industries' Output as a Percentage of Gr
[#permalink]
 09 Apr 2018, 18:56
09 Apr 2018, 18:56
6
Expert Reply
It is highly annoying how much scrolling up and down and sideways is involved in this problem. The way I did this problem without going crazy is that I clicked on the image and saved the image for both graphs so I could avoid all the scrolling. The real GRE, by the way, will never require any scrolling; you will always be able to see both graphs and your question simultaneously. Anyway.
QUESTION 1:
We're asked what percent of the mining industries' annual production came from aluminum. So we need to look at the second table. Notice that Aluminum is lumped together with Uranium and Titanium. The testmakers are hoping you'll assume they are a third each, and divide the 12% by 3 to get 4%, a wrong answer. However, we can't assume anything about the proportion of Aluminum. We don't know whether it's 99% of those three metals, or 10%. Thus the answer must be E.
QUESTION 2:
The first graph shows GDP, but it doesn't show copper. The closest we can get is that it does show Metals, which during that time period were 9% of the GDP. At this point, if you were lost, you could still take a pretty good guess. We know copper is probably not the only metal they mined, so the GDP resulting from copper alone must be less than the GDP resulting from metal, which is 9%. So the answer can't be C and must be either A or B.
Looking at the 2nd graph we see that metal has been separated into 3 categories, in a ratio of 12:22:16, with copper being the third one. So, we can make a fraction of copper out of all the metal, which must be:
16/(12+22+16) = 16/50 = 32/100
That looks pretty close to a third. Since it's a third of 9%, copper must represent 3% of the average annual GDP, and A is the answer.
QUESTION 3:
Statement I:
Note that Borate production is 15% in every time period given. However, since the annual production in millions of dollars changes every year, we should be looking at 15% of a number that is continually changing. Thus Borate production in dollars is also changing every year and this one is out.
Statement II:
To find whether 1981-1985 produced the greatest value of gold and silver, we must use find the percentage of the total production that gold and silver produced. For example, in 1981-1985, gold and silver represented 20%, or 1/5th, of that year's total of $342.5 million. The easy arithmetic trick way to find 1/5th of anything is to first divide it by 10, then multiply by 2. So dividing 342.5 by 10 we get 34.25, and multiplying by 2 we get 68.5. So gold and silver made $68.5 million that year.
There must be some kind of trick, or easy arithmetic, for each time period, so look out for them. From 1986-1990 we must find 17% of $326.8. Sloppy numbers, but notice that both the total and the percentage are smaller, so we know that this will make a smaller total and can be disregarded. From 1991-1995, we have 20% of $310 million. Since the percentage is the same but the total is smaller, we also know that this one is smaller.
From 1996-2000, we're given a very slightly larger percent of a much smaller number. The percentage has increased by 10% (of itself) while the total has decreased by something like 25% (from $342.5) so this can't be larger either. Finally, from 2001-2005, we must find 24% of $205 million. We can easily estimate this as about a quarter of about $200, giving us $50 million, which is nowhere near the $68.5 million in the first time period. Thus this statement must be true.
Statement III:
We aren't given the GDP, but we are able to calculate it for each of these years given the information in the graphs. This could be a bit of a laborious process to do 5 times, so let's try to streamline as much as possible. Using 1981-1985 as an example, one way to calculate the GDP would be to find out how much money was made by borates using the 2nd table. Then, using the first table, since we're told what percent of the GDP borates represent, we can find the total GDP. The former equation would be:
Production of borate in millions of dollars = Percent of total production x Total production = 15% x $342.5 million
The latter equation would be:
Total GDP = (Production of borate)/(% of GDP) x 100% = ((15% x 342.5)/(1.5)) x 100%
That seems pretty complicated. However, we don't need the actual amounts; we only need to compare them. We can almost treat this like a 5-part Quantitative Comparison problem. And since all five periods must be multiplied by that 100%, we can ignore it. Also, the reason I chose borate is that conveniently, the percentage for borate was 15% in all five time periods, which means it too can be ignored. So essentially we can compare all 5 time periods by dividing that period's average annual production in the second graph by borate's percentage of GDP in the first graph. That gets us:
342.5/1.5 vs. 326.8/2.25 vs. 310/2.75 vs. 257.9/2.75 vs. 205/3.1
Now, we don't need to rank these. We merely need to figure out which is the largest. Since in general, we see the numerator is getting smaller, and the denominator is getting bigger, however, we can say that the GDP in the first time period, 1981-1985, is the largest, and the GDP is gradually getting smaller until the GDP is actually the smallest in the last time period, 2001-2005. Thus this answer is out.
Long story short, only II applies.
QUESTION 1:
We're asked what percent of the mining industries' annual production came from aluminum. So we need to look at the second table. Notice that Aluminum is lumped together with Uranium and Titanium. The testmakers are hoping you'll assume they are a third each, and divide the 12% by 3 to get 4%, a wrong answer. However, we can't assume anything about the proportion of Aluminum. We don't know whether it's 99% of those three metals, or 10%. Thus the answer must be E.
QUESTION 2:
The first graph shows GDP, but it doesn't show copper. The closest we can get is that it does show Metals, which during that time period were 9% of the GDP. At this point, if you were lost, you could still take a pretty good guess. We know copper is probably not the only metal they mined, so the GDP resulting from copper alone must be less than the GDP resulting from metal, which is 9%. So the answer can't be C and must be either A or B.
Looking at the 2nd graph we see that metal has been separated into 3 categories, in a ratio of 12:22:16, with copper being the third one. So, we can make a fraction of copper out of all the metal, which must be:
16/(12+22+16) = 16/50 = 32/100
That looks pretty close to a third. Since it's a third of 9%, copper must represent 3% of the average annual GDP, and A is the answer.
QUESTION 3:
Statement I:
Note that Borate production is 15% in every time period given. However, since the annual production in millions of dollars changes every year, we should be looking at 15% of a number that is continually changing. Thus Borate production in dollars is also changing every year and this one is out.
Statement II:
To find whether 1981-1985 produced the greatest value of gold and silver, we must use find the percentage of the total production that gold and silver produced. For example, in 1981-1985, gold and silver represented 20%, or 1/5th, of that year's total of $342.5 million. The easy arithmetic trick way to find 1/5th of anything is to first divide it by 10, then multiply by 2. So dividing 342.5 by 10 we get 34.25, and multiplying by 2 we get 68.5. So gold and silver made $68.5 million that year.
There must be some kind of trick, or easy arithmetic, for each time period, so look out for them. From 1986-1990 we must find 17% of $326.8. Sloppy numbers, but notice that both the total and the percentage are smaller, so we know that this will make a smaller total and can be disregarded. From 1991-1995, we have 20% of $310 million. Since the percentage is the same but the total is smaller, we also know that this one is smaller.
From 1996-2000, we're given a very slightly larger percent of a much smaller number. The percentage has increased by 10% (of itself) while the total has decreased by something like 25% (from $342.5) so this can't be larger either. Finally, from 2001-2005, we must find 24% of $205 million. We can easily estimate this as about a quarter of about $200, giving us $50 million, which is nowhere near the $68.5 million in the first time period. Thus this statement must be true.
Statement III:
We aren't given the GDP, but we are able to calculate it for each of these years given the information in the graphs. This could be a bit of a laborious process to do 5 times, so let's try to streamline as much as possible. Using 1981-1985 as an example, one way to calculate the GDP would be to find out how much money was made by borates using the 2nd table. Then, using the first table, since we're told what percent of the GDP borates represent, we can find the total GDP. The former equation would be:
Production of borate in millions of dollars = Percent of total production x Total production = 15% x $342.5 million
The latter equation would be:
Total GDP = (Production of borate)/(% of GDP) x 100% = ((15% x 342.5)/(1.5)) x 100%
That seems pretty complicated. However, we don't need the actual amounts; we only need to compare them. We can almost treat this like a 5-part Quantitative Comparison problem. And since all five periods must be multiplied by that 100%, we can ignore it. Also, the reason I chose borate is that conveniently, the percentage for borate was 15% in all five time periods, which means it too can be ignored. So essentially we can compare all 5 time periods by dividing that period's average annual production in the second graph by borate's percentage of GDP in the first graph. That gets us:
342.5/1.5 vs. 326.8/2.25 vs. 310/2.75 vs. 257.9/2.75 vs. 205/3.1
Now, we don't need to rank these. We merely need to figure out which is the largest. Since in general, we see the numerator is getting smaller, and the denominator is getting bigger, however, we can say that the GDP in the first time period, 1981-1985, is the largest, and the GDP is gradually getting smaller until the GDP is actually the smallest in the last time period, 2001-2005. Thus this answer is out.
Long story short, only II applies.
General Discussion
Re: Natural Resource Industries' Output as a Percentage of Gr
[#permalink]
 03 Jul 2018, 02:37
03 Jul 2018, 02:37
SherpaPrep wrote:
It is highly annoying how much scrolling up and down and sideways is involved in this problem. The way I did this problem without going crazy is that I clicked on the image and saved the image for both graphs so I could avoid all the scrolling. The real GRE, by the way, will never require any scrolling; you will always be able to see both graphs and your question simultaneously. Anyway.
QUESTION 1:
We're asked what percent of the mining industries' annual production came from aluminum. So we need to look at the second table. Notice that Aluminum is lumped together with Uranium and Titanium. The testmakers are hoping you'll assume they are a third each, and divide the 12% by 3 to get 4%, a wrong answer. However, we can't assume anything about the proportion of Aluminum. We don't know whether it's 99% of those three metals, or 10%. Thus the answer must be E.
QUESTION 2:
The first graph shows GDP, but it doesn't show copper. The closest we can get is that it does show Metals, which during that time period were 9% of the GDP. At this point, if you were lost, you could still take a pretty good guess. We know copper is probably not the only metal they mined, so the GDP resulting from copper alone must be less than the GDP resulting from metal, which is 9%. So the answer can't be C and must be either A or B.
Looking at the 2nd graph we see that metal has been separated into 3 categories, in a ratio of 12:22:16, with copper being the third one. So, we can make a fraction of copper out of all the metal, which must be:
16/(12+22+16) = 16/50 = 32/100
That looks pretty close to a third. Since it's a third of 9%, copper must represent 3% of the average annual GDP, and A is the answer.
QUESTION 3:
Statement I:
Note that Borate production is 15% in every time period given. However, since the annual production in millions of dollars changes every year, we should be looking at 15% of a number that is continually changing. Thus Borate production in dollars is also changing every year and this one is out.
Statement II:
To find whether 1981-1985 produced the greatest value of gold and silver, we must use find the percentage of the total production that gold and silver produced. For example, in 1981-1985, gold and silver represented 20%, or 1/5th, of that year's total of $342.5 million. The easy arithmetic trick way to find 1/5th of anything is to first divide it by 10, then multiply by 2. So dividing 342.5 by 10 we get 34.25, and multiplying by 2 we get 68.5. So gold and silver made $68.5 million that year.
There must be some kind of trick, or easy arithmetic, for each time period, so look out for them. From 1986-1990 we must find 17% of $326.8. Sloppy numbers, but notice that both the total and the percentage are smaller, so we know that this will make a smaller total and can be disregarded. From 1991-1995, we have 20% of $310 million. Since the percentage is the same but the total is smaller, we also know that this one is smaller.
From 1996-2000, we're given a very slightly larger percent of a much smaller number. The percentage has increased by 10% (of itself) while the total has decreased by something like 25% (from $342.5) so this can't be larger either. Finally, from 2001-2005, we must find 24% of $205 million. We can easily estimate this as about a quarter of about $200, giving us $50 million, which is nowhere near the $68.5 million in the first time period. Thus this statement must be true.
Statement III:
We aren't given the GDP, but we are able to calculate it for each of these years given the information in the graphs. This could be a bit of a laborious process to do 5 times, so let's try to streamline as much as possible. Using 1981-1985 as an example, one way to calculate the GDP would be to find out how much money was made by borates using the 2nd table. Then, using the first table, since we're told what percent of the GDP borates represent, we can find the total GDP. The former equation would be:
Production of borate in millions of dollars = Percent of total production x Total production = 15% x $342.5 million
The latter equation would be:
Total GDP = (Production of borate)/(% of GDP) x 100% = ((15% x 342.5)/(1.5)) x 100%
That seems pretty complicated. However, we don't need the actual amounts; we only need to compare them. We can almost treat this like a 5-part Quantitative Comparison problem. And since all five periods must be multiplied by that 100%, we can ignore it. Also, the reason I chose borate is that conveniently, the percentage for borate was 15% in all five time periods, which means it too can be ignored. So essentially we can compare all 5 time periods by dividing that period's average annual production in the second graph by borate's percentage of GDP in the first graph. That gets us:
342.5/1.5 vs. 326.8/2.25 vs. 310/2.75 vs. 257.9/2.75 vs. 205/3.1
Now, we don't need to rank these. We merely need to figure out which is the largest. Since in general, we see the numerator is getting smaller, and the denominator is getting bigger, however, we can say that the GDP in the first time period, 1981-1985, is the largest, and the GDP is gradually getting smaller until the GDP is actually the smallest in the last time period, 2001-2005. Thus this answer is out.
Long story short, only II applies.
QUESTION 1:
We're asked what percent of the mining industries' annual production came from aluminum. So we need to look at the second table. Notice that Aluminum is lumped together with Uranium and Titanium. The testmakers are hoping you'll assume they are a third each, and divide the 12% by 3 to get 4%, a wrong answer. However, we can't assume anything about the proportion of Aluminum. We don't know whether it's 99% of those three metals, or 10%. Thus the answer must be E.
QUESTION 2:
The first graph shows GDP, but it doesn't show copper. The closest we can get is that it does show Metals, which during that time period were 9% of the GDP. At this point, if you were lost, you could still take a pretty good guess. We know copper is probably not the only metal they mined, so the GDP resulting from copper alone must be less than the GDP resulting from metal, which is 9%. So the answer can't be C and must be either A or B.
Looking at the 2nd graph we see that metal has been separated into 3 categories, in a ratio of 12:22:16, with copper being the third one. So, we can make a fraction of copper out of all the metal, which must be:
16/(12+22+16) = 16/50 = 32/100
That looks pretty close to a third. Since it's a third of 9%, copper must represent 3% of the average annual GDP, and A is the answer.
QUESTION 3:
Statement I:
Note that Borate production is 15% in every time period given. However, since the annual production in millions of dollars changes every year, we should be looking at 15% of a number that is continually changing. Thus Borate production in dollars is also changing every year and this one is out.
Statement II:
To find whether 1981-1985 produced the greatest value of gold and silver, we must use find the percentage of the total production that gold and silver produced. For example, in 1981-1985, gold and silver represented 20%, or 1/5th, of that year's total of $342.5 million. The easy arithmetic trick way to find 1/5th of anything is to first divide it by 10, then multiply by 2. So dividing 342.5 by 10 we get 34.25, and multiplying by 2 we get 68.5. So gold and silver made $68.5 million that year.
There must be some kind of trick, or easy arithmetic, for each time period, so look out for them. From 1986-1990 we must find 17% of $326.8. Sloppy numbers, but notice that both the total and the percentage are smaller, so we know that this will make a smaller total and can be disregarded. From 1991-1995, we have 20% of $310 million. Since the percentage is the same but the total is smaller, we also know that this one is smaller.
From 1996-2000, we're given a very slightly larger percent of a much smaller number. The percentage has increased by 10% (of itself) while the total has decreased by something like 25% (from $342.5) so this can't be larger either. Finally, from 2001-2005, we must find 24% of $205 million. We can easily estimate this as about a quarter of about $200, giving us $50 million, which is nowhere near the $68.5 million in the first time period. Thus this statement must be true.
Statement III:
We aren't given the GDP, but we are able to calculate it for each of these years given the information in the graphs. This could be a bit of a laborious process to do 5 times, so let's try to streamline as much as possible. Using 1981-1985 as an example, one way to calculate the GDP would be to find out how much money was made by borates using the 2nd table. Then, using the first table, since we're told what percent of the GDP borates represent, we can find the total GDP. The former equation would be:
Production of borate in millions of dollars = Percent of total production x Total production = 15% x $342.5 million
The latter equation would be:
Total GDP = (Production of borate)/(% of GDP) x 100% = ((15% x 342.5)/(1.5)) x 100%
That seems pretty complicated. However, we don't need the actual amounts; we only need to compare them. We can almost treat this like a 5-part Quantitative Comparison problem. And since all five periods must be multiplied by that 100%, we can ignore it. Also, the reason I chose borate is that conveniently, the percentage for borate was 15% in all five time periods, which means it too can be ignored. So essentially we can compare all 5 time periods by dividing that period's average annual production in the second graph by borate's percentage of GDP in the first graph. That gets us:
342.5/1.5 vs. 326.8/2.25 vs. 310/2.75 vs. 257.9/2.75 vs. 205/3.1
Now, we don't need to rank these. We merely need to figure out which is the largest. Since in general, we see the numerator is getting smaller, and the denominator is getting bigger, however, we can say that the GDP in the first time period, 1981-1985, is the largest, and the GDP is gradually getting smaller until the GDP is actually the smallest in the last time period, 2001-2005. Thus this answer is out.
Long story short, only II applies.
Thank you for this in-depth explanation. For statement three, i am still not sure unfortunately about why you choose approach. In general, i am a little bit confused about statement's solution.






