
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
How many factors greater than 1 do 120, 210, and 270 have in
[#permalink]
 12 Aug 2018, 15:31
12 Aug 2018, 15:31
1
Expert Reply
8
Bookmarks
Question Stats:
 39% (01:55) correct
39% (01:55) correct
 60% (01:34) wrong
60% (01:34) wrong  based on 99 sessions
based on 99 sessions
Hide Show timer Statistics
How many factors greater than 1 do 120, 210, and 270 have in common?
(A) One
(B) Three
(C) Six
(D) Seven
(E) Thirty
(A) One
(B) Three
(C) Six
(D) Seven
(E) Thirty
Re: How many factors greater than 1 do 120, 210, and 270 have in
[#permalink]
 04 Apr 2020, 22:31
04 Apr 2020, 22:31
4
3
Bookmarks
This is the other way to do it
120 = 10 * 12 = 2*5*3*2
210 = 3*7*2*5
270 = 3*3*3*2*5
Find common prime factors in all three numbers above: 2^1 * 3^1 * 5^1. So to find all factors add 1 onto each exponent and multiply altogether (1+1)*(1+1)*(1+1) = 8. But we don't want 1. So 8 - 1 = 7
120 = 10 * 12 = 2*5*3*2
210 = 3*7*2*5
270 = 3*3*3*2*5
Find common prime factors in all three numbers above: 2^1 * 3^1 * 5^1. So to find all factors add 1 onto each exponent and multiply altogether (1+1)*(1+1)*(1+1) = 8. But we don't want 1. So 8 - 1 = 7
General Discussion
Re: How many factors greater than 1 do 120, 210, and 270 have in
[#permalink]
 15 Aug 2018, 05:14
15 Aug 2018, 05:14
Expert Reply
Explanation
Pick one of the numbers and list all of its factors. The factors of 120 are: 1 & 120, 2 & 60, 3 & 40, 4 & 30, 5 & 24, 6 & 20, 8 & 15, 10 & 12. Since the problem specifically asks for factors “greater than 1,” eliminate 1 now. Now cross off any factors that do not go into 210:
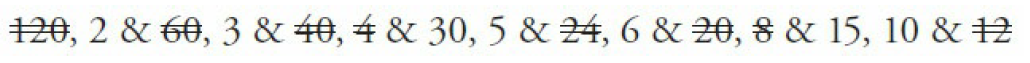
Capture.PNG [ 103.47 KiB | Viewed 11996 times ]
Now cross off any factors remaining that do not go into 270. Interestingly, all of the remaining factors (2, 3, 5, 6, 10, 15, 30) do go into 270. There are 7 shared factors.
Pick one of the numbers and list all of its factors. The factors of 120 are: 1 & 120, 2 & 60, 3 & 40, 4 & 30, 5 & 24, 6 & 20, 8 & 15, 10 & 12. Since the problem specifically asks for factors “greater than 1,” eliminate 1 now. Now cross off any factors that do not go into 210:
Attachment:
Capture.PNG [ 103.47 KiB | Viewed 11996 times ]
Now cross off any factors remaining that do not go into 270. Interestingly, all of the remaining factors (2, 3, 5, 6, 10, 15, 30) do go into 270. There are 7 shared factors.








