GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
In the figure, the areas of parallelograms EBFD and AECF are
[#permalink]
01 Oct 2018, 13:44
01 Oct 2018, 13:44
Expert Reply
4
Bookmarks
00:00
Question Stats:
89% (01:53) correct
10% (02:09) wrong based on 28 sessions
Hide Show timer Statistics
Attachment:
#GREpracticequestin In the figure, the areas of parallelograms EBFD .jpg [ 30.48 KiB | Viewed 4704 times ]
In the figure, the areas of parallelograms EBFD and AECF are 3 and 2, respectively. What is the area of rectangle ABCD ?
(A) 3
(B) 4
(C) 5
(D) \(4 \sqrt{3}\)
(E) 7
Re: In the figure, the areas of parallelograms EBFD and AECF are
[#permalink]
02 Oct 2018, 06:12
02 Oct 2018, 06:12
solution pls??
Re: In the figure, the areas of parallelograms EBFD and AECF are
[#permalink]
03 Oct 2018, 13:31
03 Oct 2018, 13:31
3
Expert Reply
Let DF be x and FC be y and the height of the rectangle (BC) be h. Asshown in figure below:
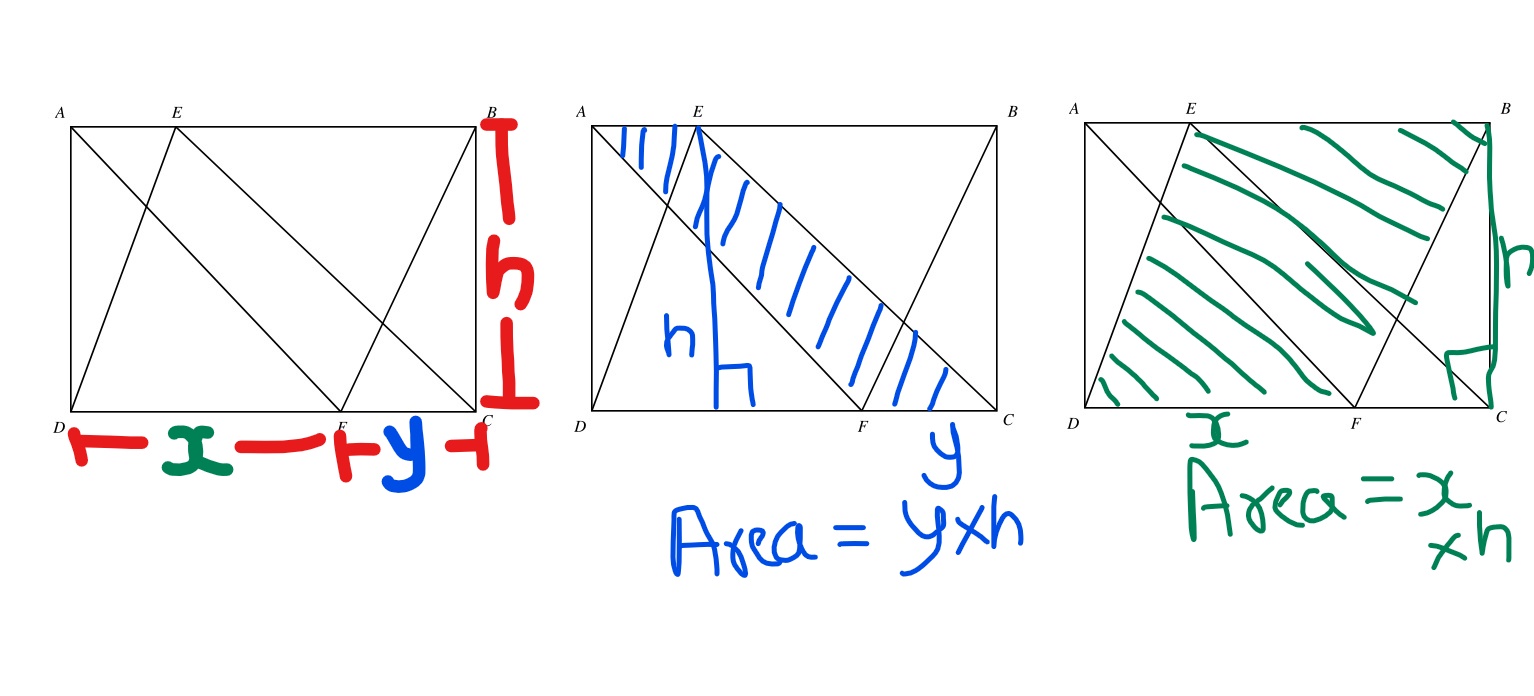
Inkedrectangle_LI.jpg [ 567 KiB | Viewed 5889 times ]
Now area AECF =2 and writing it in terms of our variable we get
area AECF =2= \(y \times h\).
Similarly area EBFD =3 and writing it in terms of our variable we get
area EBFD =3= \(x \times h\).
Now area of the rectangle is clearly =\((x+y) \times h\).
Clearly if we add the area of EBFD and AECF we get the area of rectangle = \((x+y) \times h= x \times h + y \times h = 3+2= 5\)
Hence option C
Attachment:
Inkedrectangle_LI.jpg [ 567 KiB | Viewed 5889 times ]
Now area AECF =2 and writing it in terms of our variable we get
area AECF =2= \(y \times h\).
Similarly area EBFD =3 and writing it in terms of our variable we get
area EBFD =3= \(x \times h\).
Now area of the rectangle is clearly =\((x+y) \times h\).
Clearly if we add the area of EBFD and AECF we get the area of rectangle = \((x+y) \times h= x \times h + y \times h = 3+2= 5\)
Hence option C
