
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
For how many integer values of x
[#permalink]
 08 Jun 2019, 05:50
08 Jun 2019, 05:50
1
1
7
Bookmarks
Question Stats:
 52% (02:21) correct
52% (02:21) correct
 47% (01:50) wrong
47% (01:50) wrong  based on 44 sessions
based on 44 sessions
Hide Show timer Statistics
For how many integer values of x, is |2x−5|+|x+1|+|x|<10?
A. 1
B. 2
C. 4
D. 5
E. Infinite
A. 1
B. 2
C. 4
D. 5
E. Infinite
Re: For how many integer values of x
[#permalink]
 09 Jun 2019, 10:17
09 Jun 2019, 10:17
1
Expert Reply
Taking all positive terms :
\(2x-5+x+1+x<10\)
\(4x-4<10\)
\(x<\frac{7}{2}\)
Taking all negative terms :
\(5-2x-x-x-x<10\)
\(x>-\frac{3}{2}\)
So the range is \(-\frac{3}{2}<x<\frac{7}{2}\)
Therefore , the possible values are -1,0,1,2,3...so 5 values
\(2x-5+x+1+x<10\)
\(4x-4<10\)
\(x<\frac{7}{2}\)
Taking all negative terms :
\(5-2x-x-x-x<10\)
\(x>-\frac{3}{2}\)
So the range is \(-\frac{3}{2}<x<\frac{7}{2}\)
Therefore , the possible values are -1,0,1,2,3...so 5 values
Moderator

Joined: 02 Jan 2020
Status:GRE Quant Tutor
Posts: 1141
Given Kudos: 9
Location: India
Concentration: General Management
Schools: XLRI Jamshedpur, India - Class of 2014
GMAT 1: 700 Q51 V31
GPA: 2.8
WE:Engineering (Computer Software)
For how many integer values of x
[#permalink]
 24 Dec 2021, 10:57
24 Dec 2021, 10:57
Given that |2x−5|+|x+1|+|x|<10 and we need to find how many integer values can x take
When we have multiple Absolute values in a problem then we need to reduce the number of cases. Let's see how to do that.
Lets find out the points on the number line where the values inside each absolute value will change sign.
We can do that by putting each term inside the absolute value individually equal to zero.
For |2x-5| -> 2x-5 = 0 => x = \(\frac{5}{2}\) = 2.5
For |x+1| -> x+1 = 0 => x = -1
For |x| -> x = 0
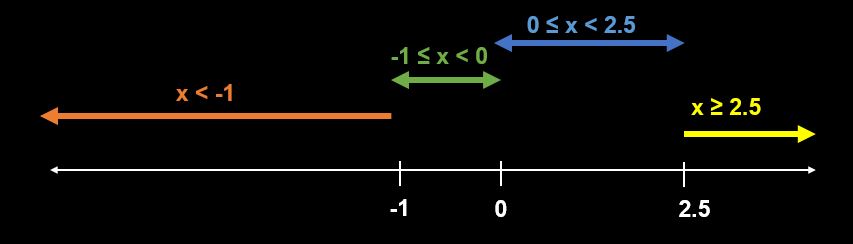
problem.JPG [ 20.43 KiB | Viewed 3043 times ]
Case 1: x < -1
Let's take any value of x < -1, lets say -2 and substitute and see whether the values inside the absolute value is +ve or -ve or 0
For |2x-5| -> (2*-2)-5 = -9 => -ve =>|2x-5| = -(2x-5)
For |x+1| -> -2+1 = -1 => -ve => |x+1| = -(x+1)
For |x| -> -2 => -ve => |x| = -x
|2x−5|+|x+1|+|x|<10 => -(2x-5) - (x+1) -x < 10
=> -2x + 5 -x - 1 -x < 10
=> -4x < 10 -4
=> -4x < 6 => x > \(\frac{-6}{4}\) => x > -1.5
And conditions was x < -1
So, intersection will be -1.5 < x < -1 => NO Integer solution in this range
Case 2: -1 ≤ x < 0
Let's take any value of x which satisfies -1 ≤ x < 0, lets say -0.5 and substitute and see whether the values inside the absolute value is +ve or -ve or 0
For |2x-5| -> (2*-0.5)-5 => -ve =>|2x-5| = -(2x-5)
For |x+1| -> -0.5+1 => +ve => |x+1| = x+1
For |x| -> -0.5 => -ve => |x| = -x
|2x−5|+|x+1|+|x|<10 => -(2x-5) + (x+1) -x < 10
=> -2x + 5 + x + 1 -x < 10
=> -2x < 10 -6
=> -2x < 4 => x > \(\frac{-4}{2}\) => x > -2
And conditions was -1 ≤ x < 0
So, intersection will be -1 ≤ x < 0 => x=-1 is an integer solution in this range
Case 3: 0 ≤ x < 2.5
Let's take any value of x which satisfies 0 ≤ x < 2.5, lets say 1 and substitute and see whether the values inside the absolute value is +ve or -ve or 0
For |2x-5| -> (2*1)-5 => -ve =>|2x-5| = -(2x-5)
For |x+1| -> 1+1 => +ve => |x+1| = x+1
For |x| -> 1 => +ve => |x| = x
|2x−5|+|x+1|+|x|<10 => -(2x-5) + (x+1) + x < 10
=> -2x + 5 + x + 1 + x < 10
=> 6 < 10
Which is always true
So, entire range 0 ≤ x < 2.5 is possible
x=0, 1, 2 are integer solution in this range
Case 4: x ≥ 2.5
Let's take any value of x which satisfies x ≥ 2.5, lets say 10 and substitute and see whether the values inside the absolute value is +ve or -ve or 0
For |2x-5| -> (2*10)-5 => +ve =>|2x-5| = 2x-5
For |x+1| -> 10+1 => +ve => |x+1| = x+1
For |x| -> 10 => +ve => |x| = x
|2x−5|+|x+1|+|x|<10 => 2x-5 + (x+1) + x < 10
=> 2x - 5 + x + 1 + x < 10
=> 4x - 4 < 10
=> 4x < 14
=> x < \(\frac{14}{4}\)
=> x < 3.5
And conditions was x ≥ 2.5
So, intersection will be 2.5 ≤ x < 3.5=> x=3 is an integer solution in this range
So, integer values which are possible are -1 , 0, 1, 2, 3
=> 5 values
So, Answer will be D
Hope it helps!
Watch the following video to learn how to Solve Inequality + Absolute value Problems
When we have multiple Absolute values in a problem then we need to reduce the number of cases. Let's see how to do that.
Lets find out the points on the number line where the values inside each absolute value will change sign.
We can do that by putting each term inside the absolute value individually equal to zero.
For |2x-5| -> 2x-5 = 0 => x = \(\frac{5}{2}\) = 2.5
For |x+1| -> x+1 = 0 => x = -1
For |x| -> x = 0
Attachment:
problem.JPG [ 20.43 KiB | Viewed 3043 times ]
Case 1: x < -1
Let's take any value of x < -1, lets say -2 and substitute and see whether the values inside the absolute value is +ve or -ve or 0
For |2x-5| -> (2*-2)-5 = -9 => -ve =>|2x-5| = -(2x-5)
For |x+1| -> -2+1 = -1 => -ve => |x+1| = -(x+1)
For |x| -> -2 => -ve => |x| = -x
|2x−5|+|x+1|+|x|<10 => -(2x-5) - (x+1) -x < 10
=> -2x + 5 -x - 1 -x < 10
=> -4x < 10 -4
=> -4x < 6 => x > \(\frac{-6}{4}\) => x > -1.5
And conditions was x < -1
So, intersection will be -1.5 < x < -1 => NO Integer solution in this range
Case 2: -1 ≤ x < 0
Let's take any value of x which satisfies -1 ≤ x < 0, lets say -0.5 and substitute and see whether the values inside the absolute value is +ve or -ve or 0
For |2x-5| -> (2*-0.5)-5 => -ve =>|2x-5| = -(2x-5)
For |x+1| -> -0.5+1 => +ve => |x+1| = x+1
For |x| -> -0.5 => -ve => |x| = -x
|2x−5|+|x+1|+|x|<10 => -(2x-5) + (x+1) -x < 10
=> -2x + 5 + x + 1 -x < 10
=> -2x < 10 -6
=> -2x < 4 => x > \(\frac{-4}{2}\) => x > -2
And conditions was -1 ≤ x < 0
So, intersection will be -1 ≤ x < 0 => x=-1 is an integer solution in this range
Case 3: 0 ≤ x < 2.5
Let's take any value of x which satisfies 0 ≤ x < 2.5, lets say 1 and substitute and see whether the values inside the absolute value is +ve or -ve or 0
For |2x-5| -> (2*1)-5 => -ve =>|2x-5| = -(2x-5)
For |x+1| -> 1+1 => +ve => |x+1| = x+1
For |x| -> 1 => +ve => |x| = x
|2x−5|+|x+1|+|x|<10 => -(2x-5) + (x+1) + x < 10
=> -2x + 5 + x + 1 + x < 10
=> 6 < 10
Which is always true
So, entire range 0 ≤ x < 2.5 is possible
x=0, 1, 2 are integer solution in this range
Case 4: x ≥ 2.5
Let's take any value of x which satisfies x ≥ 2.5, lets say 10 and substitute and see whether the values inside the absolute value is +ve or -ve or 0
For |2x-5| -> (2*10)-5 => +ve =>|2x-5| = 2x-5
For |x+1| -> 10+1 => +ve => |x+1| = x+1
For |x| -> 10 => +ve => |x| = x
|2x−5|+|x+1|+|x|<10 => 2x-5 + (x+1) + x < 10
=> 2x - 5 + x + 1 + x < 10
=> 4x - 4 < 10
=> 4x < 14
=> x < \(\frac{14}{4}\)
=> x < 3.5
And conditions was x ≥ 2.5
So, intersection will be 2.5 ≤ x < 3.5=> x=3 is an integer solution in this range
So, integer values which are possible are -1 , 0, 1, 2, 3
=> 5 values
So, Answer will be D
Hope it helps!
Watch the following video to learn how to Solve Inequality + Absolute value Problems






