
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Chocolates are packed in boxes that measure six inches long,
[#permalink]
 Updated on: 20 Oct 2018, 03:24
Updated on: 20 Oct 2018, 03:24
1
6
Bookmarks
Question Stats:
 13% (02:20) correct
13% (02:20) correct
 86% (02:55) wrong
86% (02:55) wrong  based on 43 sessions
based on 43 sessions
Hide Show timer Statistics
Chocolates are packed in boxes that measure six inches long, three inches wide, and two inches high. If four individual boxes are packaged together in bulk by either arranging them in a single row or stacking them, what could be the total surface area of the bulk unit?
Indicate ALL that apply.
[ ] 168
[ ] 180
[ ] 192
[ ] 204
[ ] 252
[ ] 294
Indicate ALL that apply.
[ ] 168
[ ] 180
[ ] 192
[ ] 204
[ ] 252
[ ] 294
ShowHide Answer
Official Answer
A,B,C,E
Originally posted by amitmathew on 19 Oct 2018, 03:28.
Last edited by chetan2u on 20 Oct 2018, 03:24, edited 2 times in total.
Last edited by chetan2u on 20 Oct 2018, 03:24, edited 2 times in total.
Updated the OA
Re: Chocolates are packed in boxes that measure six inches long,
[#permalink]
 19 Oct 2018, 22:17
19 Oct 2018, 22:17
3
Expert Reply
2
Bookmarks
amitmathew wrote:
Chocolates are packed in boxes that measure six inches long, three inches wide, and two inches high. If four individual boxes are packaged together in bulk by either arranging them in a single row or stacking them, what could be the total surface area of the bulk unit?
Indicate ALL that apply.
[ ] 168
[ ] 180
[ ] 192
[ ] 204
[ ] 252
[ ] 294
Indicate ALL that apply.
[ ] 168
[ ] 180
[ ] 192
[ ] 204
[ ] 252
[ ] 294
The total surface area ÷4*SA of one box = 4*2*(6*2+2*3+6*3)=4*2*36=288
Now let us check cases when they are in single row..
The base 6*3 will always be open to air
Case I..
The faces 2*3 are placed next to each other, so there will be 3 overlaps in four boxes with the result that SIX 3*2 faces will be eliminated while calculating SA
So 288-6*(2*3)=288-36=252
Case II..
The faces 2*6 are placed next to each other, so there will be 3 overlaps in four boxes with the result that SIX 6*2 faces will be eliminated while calculating SA
So 288-6*(2*6)=288-72=216
Now let us check cases when they are in single stack..
The base 6*3 will now be merged with each other
Case I..
The faces 6*3 are placed on top of each other, so there will be 3 overlaps in four boxes with the result that SIX 3*6 faces will be eliminated while calculating SA
So 288-6*(6*3)=288-108=180
So answer would be 180,216 and 252
But if stacking means they can be in form of 2*2, so nice it does not mention that they are stacked in one column, here four faces will be 6*3 that will be eliminated and other 4 will be
The two more cases..
Case 1.. when the overlap is 2*3 faces
So eliminated SA = 4*(2*3+6*3)=4*24=96
So SA = 288-96=192
Case 2.. when the overlap is 2*6 faces
So eliminated SA = 4*(2*6+6*3)=4*30=120
So SA = 288-120=168
So 168, 180, 192, 216, 252
General Discussion
Re: Chocolates are packed in boxes that measure six inches long,
[#permalink]
 19 Oct 2018, 18:04
19 Oct 2018, 18:04
1
Expert Reply
Draw out the figure.
Blue is one choc bar. Red, Green, and Black are 3 possible configurations.
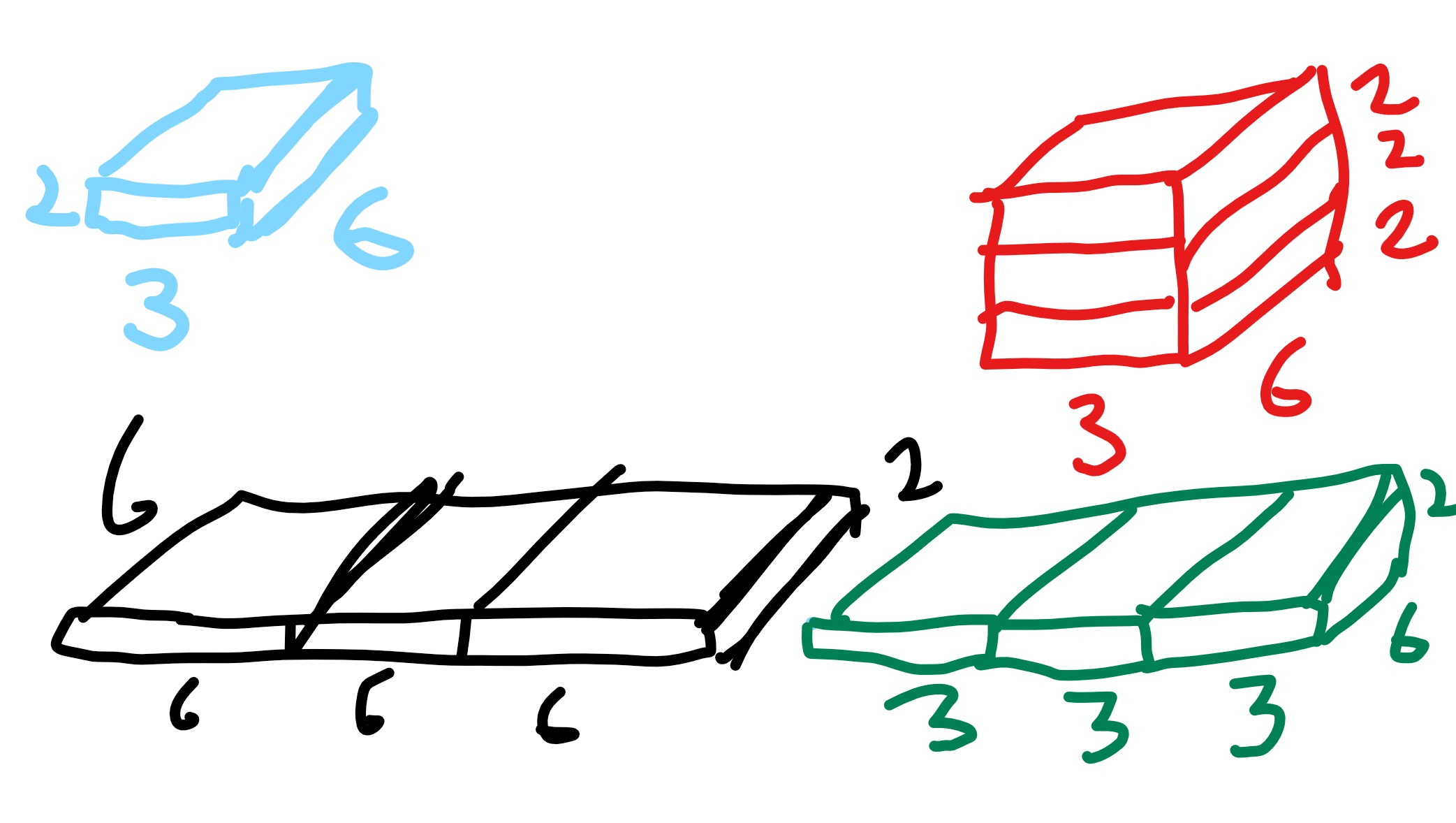
Inkednew_LI.jpg [ 729.03 KiB | Viewed 5975 times ]
NOTE: I have drawn 3 boxes but the question asks for 4 so please modify the calculation accordingly.
Now area of cuboid is given by = 2 (lw + wh + hl) where:
displayImage.jpeg [ 4.98 KiB | Viewed 6019 times ]
Red area= \(180 in^2\)
Green area= \(216 in^2\)
Black area= \(252 in^2\)
Hence 180 and 252 are correct!
Blue is one choc bar. Red, Green, and Black are 3 possible configurations.
Attachment:
Inkednew_LI.jpg [ 729.03 KiB | Viewed 5975 times ]
NOTE: I have drawn 3 boxes but the question asks for 4 so please modify the calculation accordingly.
Now area of cuboid is given by = 2 (lw + wh + hl) where:
Attachment:
displayImage.jpeg [ 4.98 KiB | Viewed 6019 times ]
Red area= \(180 in^2\)
Green area= \(216 in^2\)
Black area= \(252 in^2\)
Hence 180 and 252 are correct!









