GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Given two intersecting circles..
[#permalink]
Updated on: 20 Jan 2019, 11:50
Updated on: 20 Jan 2019, 11:50
1
5
Bookmarks
00:00
Question Stats:
65% (02:16) correct
34% (03:12) wrong based on 29 sessions
Hide Show timer Statistics
Given two intersecting circles, one with radius 15 and another with radius 25. If the distance between the two intersecting points is 20, then find the distance between the centers of the two circles?
Show: :: OA
34.09
Originally posted by Sonalika42 on 28 Aug 2016, 04:55.
Last edited by Carcass on 20 Jan 2019, 11:50, edited 1 time in total.
Last edited by Carcass on 20 Jan 2019, 11:50, edited 1 time in total.
Edited by Carcass
Re: Given two intersecting circles..
[#permalink]
01 Oct 2018, 13:22
01 Oct 2018, 13:22
5
Expert Reply
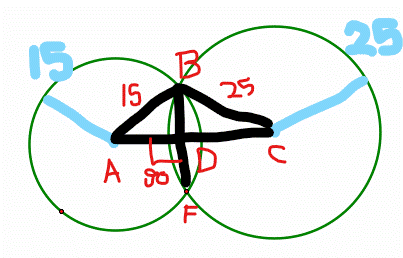
In this case let the circles intersect at B and F respectively, as shown in figure below:
Inkedintersecting.gif [ 17.93 KiB | Viewed 6659 times ]
Now line AC is a perpedicular bisector of BF at point D and AB=15 and BC=25. Hence to find the distance we need to calculate AD and DC.
Now triangle ABD is right triangle AD=\(\sqrt{AB^2-BD^2}=\sqrt{15^2-10^2}=11.18\)
Now triangle CBD is right triangle CD=\(\sqrt{BC^2-BD^2}=\sqrt{25^2-10^2}=22.91\).
Hence total distance AC = 11.18+22.91=34.09.
The portion marked in red are properties of a circle.
Attachment:
Inkedintersecting.gif [ 17.93 KiB | Viewed 6659 times ]
Now line AC is a perpedicular bisector of BF at point D and AB=15 and BC=25. Hence to find the distance we need to calculate AD and DC.
Now triangle ABD is right triangle AD=\(\sqrt{AB^2-BD^2}=\sqrt{15^2-10^2}=11.18\)
Now triangle CBD is right triangle CD=\(\sqrt{BC^2-BD^2}=\sqrt{25^2-10^2}=22.91\).
Hence total distance AC = 11.18+22.91=34.09.
The portion marked in red are properties of a circle.
