
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A certain pregnancy test comes back positive for 95 percent
[#permalink]
 13 Aug 2020, 01:29
13 Aug 2020, 01:29
1
Expert Reply
24
Bookmarks
Question Stats:
 52% (02:15) correct
52% (02:15) correct
 47% (02:07) wrong
47% (02:07) wrong  based on 148 sessions
based on 148 sessions
Hide Show timer Statistics
A certain pregnancy test comes back positive for 95 percent of pregnant women who take it. However, it also comes back positive for 5 percent of non-pregnant women who take it. Two percent of the female population of city A is pregnant. Marisa, a resident of city A, takes the pregnancy test and gets a positive result.
A)The quantity in Column A is greater.
B)The quantity in Column B is greater.
C)The two quantities are equal.
D)The relationship cannot be determined from the information given.
KUDOS for the right solution and explanation
Quantity A |
Quantity B |
The probability that Marisa is pregnant |
75 % |
A)The quantity in Column A is greater.
B)The quantity in Column B is greater.
C)The two quantities are equal.
D)The relationship cannot be determined from the information given.
KUDOS for the right solution and explanation
A certain pregnancy test comes back positive for 95 percent
[#permalink]
 14 Feb 2022, 04:30
14 Feb 2022, 04:30
2
1
Bookmarks
For the sake of clarity, I've amended the last sentence of the prompt and the wording for Quantity A:
This is an EITHER-OR problem.
Every female resident is EITHER pregnant OR not.
The test result for every female resident is EITHER positive OR negative.
For an either-or problem, use a MATRIX to organize the data, as shown below:

Screen Shot 2022-02-14 at 7.00.32 AM.png [ 61.52 KiB | Viewed 5416 times ]
Two percent of the female population of city A is pregnant.
Let the total number of women = 10,000.
Since 2% of these 10,000 women are pregnant, the following matrix is yielded:

Screen Shot 2022-02-14 at 7.04.01 AM.png [ 65.4 KiB | Viewed 5382 times ]
A certain pregnancy test comes back positive for 95 percent of pregnant women who take it.
However, it also comes back positive for 5 percent of non-pregnant women who take it.
In the preceding matrix:
A negative result is yielded for 5% of the 200 pregnant women = 10 women
A positive result is yielded for 5% of the 9,800 non-pregnant women = 490 women
The following matrix is yielded:
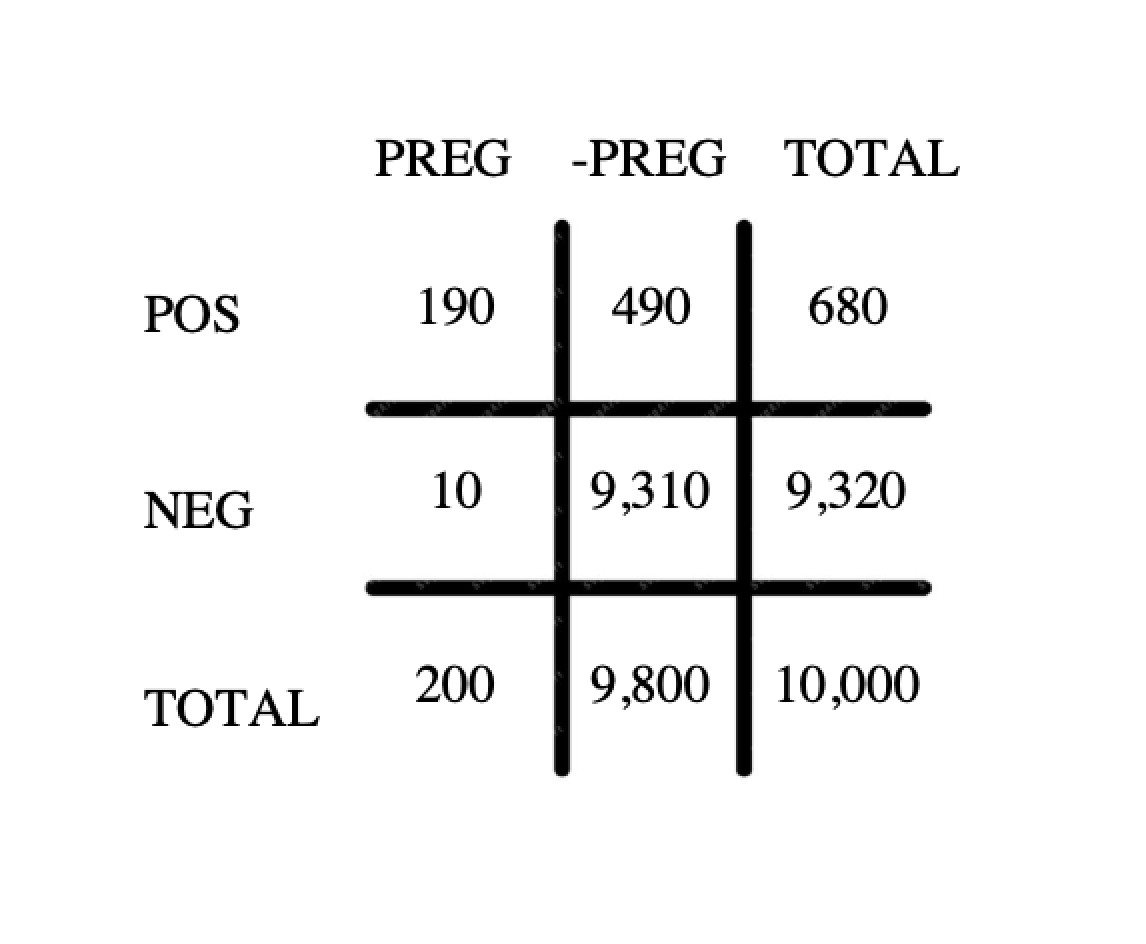
Screen Shot 2022-02-14 at 7.11.20 AM.png [ 72.83 KiB | Viewed 5409 times ]
In the resulting matrix, 190 of the 680 positive results are yielded by pregnant women.
Thus:
The probability that Marissa's positive result indicates an actual pregnancy = 190/680 = much less than 75%.
Quantity B is larger.
Carcass wrote:
A certain pregnancy test comes back positive for 95 percent of pregnant women who take it. However, it also comes back positive for 5 percent of non-pregnant women who take it. Two percent of the female population of city A is pregnant. Yesterday, every woman who resides in city A took the test, and Marisa, a female resident of city A, got a positive result.
Quantity A |
Quantity B |
The probability that Marisa's test indicated an actual pregnancy |
75 % |
This is an EITHER-OR problem.
Every female resident is EITHER pregnant OR not.
The test result for every female resident is EITHER positive OR negative.
For an either-or problem, use a MATRIX to organize the data, as shown below:
Attachment:
Screen Shot 2022-02-14 at 7.00.32 AM.png [ 61.52 KiB | Viewed 5416 times ]
Two percent of the female population of city A is pregnant.
Let the total number of women = 10,000.
Since 2% of these 10,000 women are pregnant, the following matrix is yielded:
Attachment:
Screen Shot 2022-02-14 at 7.04.01 AM.png [ 65.4 KiB | Viewed 5382 times ]
A certain pregnancy test comes back positive for 95 percent of pregnant women who take it.
However, it also comes back positive for 5 percent of non-pregnant women who take it.
In the preceding matrix:
A negative result is yielded for 5% of the 200 pregnant women = 10 women
A positive result is yielded for 5% of the 9,800 non-pregnant women = 490 women
The following matrix is yielded:
Attachment:
Screen Shot 2022-02-14 at 7.11.20 AM.png [ 72.83 KiB | Viewed 5409 times ]
In the resulting matrix, 190 of the 680 positive results are yielded by pregnant women.
Thus:
The probability that Marissa's positive result indicates an actual pregnancy = 190/680 = much less than 75%.
Quantity B is larger.
Show: ::
B
General Discussion
Re: A certain pregnancy test comes back positive for 95 percent
[#permalink]
 13 Aug 2020, 14:08
13 Aug 2020, 14:08
4
Event + = positive result
Event - = negative result
Event P= woman is pregnant
Event NP= woman is not pregnant
Given:
We are told that given you are pregnant the test results positive 95% of the time. Therefore
Pr(+|P)=.95
We are told that given you are not pregnant the test results positive 5% of the time. Therefore
Pr(+|NP)=.05
We are told 2% of the population is pregnant Therefore
Pr(P)=.02
Pr(NP)=.98
We are looking for: Given that Marissa tested positive what is the probability she is pregnant?
That is, we are looking for: Pr(P|+)
Pr(P|+)
=Pr(P,+)/Pr(+)
Notice
Pr(+|P)=Pr(P,+)/Pr(P)
Therefore Pr(p,+)=Pr(P)Pr(+|P)
Also
Pr(+|NP)=Pr(NP,+)/Pr(NP)
Therefore Pr(NP,+)=Pr(NP)Pr(+|NP)
Also
Pr(+)=Pr(P,+)+Pr(NP,+)=Pr(P)Pr(+|P)+Pr(NP)Pr(+|NP)
So we get
Pr(P|+)
=Pr(P,+)/Pr(+)
=Pr(P)Pr(+|P)/ [Pr(P)Pr(+|P)+Pr(NP)Pr(+|NP)]
=(.02)(.95)/ [(.02)*(.95) + (.98)(.05)]
= .019/(.019+ .049)
= .279
.279<.75
Final Answer: B
PS: This is definitely not on the GRE. This question required Bayes Theorem and Law of Total Probability, both of which are out of scope for the GRE.
Event - = negative result
Event P= woman is pregnant
Event NP= woman is not pregnant
Given:
We are told that given you are pregnant the test results positive 95% of the time. Therefore
Pr(+|P)=.95
We are told that given you are not pregnant the test results positive 5% of the time. Therefore
Pr(+|NP)=.05
We are told 2% of the population is pregnant Therefore
Pr(P)=.02
Pr(NP)=.98
We are looking for: Given that Marissa tested positive what is the probability she is pregnant?
That is, we are looking for: Pr(P|+)
Pr(P|+)
=Pr(P,+)/Pr(+)
Notice
Pr(+|P)=Pr(P,+)/Pr(P)
Therefore Pr(p,+)=Pr(P)Pr(+|P)
Also
Pr(+|NP)=Pr(NP,+)/Pr(NP)
Therefore Pr(NP,+)=Pr(NP)Pr(+|NP)
Also
Pr(+)=Pr(P,+)+Pr(NP,+)=Pr(P)Pr(+|P)+Pr(NP)Pr(+|NP)
So we get
Pr(P|+)
=Pr(P,+)/Pr(+)
=Pr(P)Pr(+|P)/ [Pr(P)Pr(+|P)+Pr(NP)Pr(+|NP)]
=(.02)(.95)/ [(.02)*(.95) + (.98)(.05)]
= .019/(.019+ .049)
= .279
.279<.75
Final Answer: B
PS: This is definitely not on the GRE. This question required Bayes Theorem and Law of Total Probability, both of which are out of scope for the GRE.







