GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Working together at their respective constant rates, robot A
[#permalink]
06 Jul 2018, 16:20
06 Jul 2018, 16:20
Expert Reply
6
Bookmarks
00:00
Question Stats:
72% (02:17) correct
27% (02:37) wrong based on 116 sessions
Hide Show timer Statistics
Working together at their respective constant rates, robot A and robot B polish 88 pounds of gemstones in 6 minutes. If robot A’s rate of polishing is \(\frac{3}{5}\)that of robot B, how many minutes would it take robot A alone to polish 165 pounds of gemstones?
(A) 15.75
(B) 18
(C) 18.75
(D) 27.5
(E) 30
(A) 15.75
(B) 18
(C) 18.75
(D) 27.5
(E) 30
Re: Working together at their respective constant rates, robot A
[#permalink]
07 Jul 2018, 19:10
07 Jul 2018, 19:10
2
1
Bookmarks
Let us assume,
Machine B can do x work in 1 min
or, Machine B can do \(6x\) work in \(6 min\)
It follows that Machine A is only 3/5 efficient as machine A hence,
Machine A can do \(\frac{18}{5} x work in 6 min.\)
From question,
\(\frac{18}{5} x + 6x = 88\)
because working together the two machines can polish \(88 pounds\) of gemstone in \(6 min.\)
solving for x we get \(x = \frac{440}{48}\)
This is the pound of gemstone machine B can polish in 1 min.
The amount of gemstone that machine A can polish in 1 min is \(\frac{440}{48} * \frac{3}{5}\)
Hence, machine A can polish \(\frac{1320}{240}\) pound of gemstone in 1 min.
or, Machine A can polish 1 pound of gemstone in \(\frac{240}{1320}\) min
or, Machine A can polish 165 pound of gemstone in \(\frac{240}{1320} * 165\) min = 30 min
Machine B can do x work in 1 min
or, Machine B can do \(6x\) work in \(6 min\)
It follows that Machine A is only 3/5 efficient as machine A hence,
Machine A can do \(\frac{18}{5} x work in 6 min.\)
From question,
\(\frac{18}{5} x + 6x = 88\)
because working together the two machines can polish \(88 pounds\) of gemstone in \(6 min.\)
solving for x we get \(x = \frac{440}{48}\)
This is the pound of gemstone machine B can polish in 1 min.
The amount of gemstone that machine A can polish in 1 min is \(\frac{440}{48} * \frac{3}{5}\)
Hence, machine A can polish \(\frac{1320}{240}\) pound of gemstone in 1 min.
or, Machine A can polish 1 pound of gemstone in \(\frac{240}{1320}\) min
or, Machine A can polish 165 pound of gemstone in \(\frac{240}{1320} * 165\) min = 30 min
Re: Working together at their respective constant rates, robot A
[#permalink]
10 Jul 2018, 06:12
10 Jul 2018, 06:12
2
Expert Reply
Explanation
When rate problems involve multiple situations, it can help to set up an initial “skeleton” W= RT chart for the solution. That way, you can determine what data is needed and fill in that data as you find it. Since the question asks how long robot A will take alone, the chart will look like this:
image1.jpg [ 26.04 KiB | Viewed 10355 times ]
Work is known and the question asks for time, so robot A’s rate is needed. Call the rates a and b. Now set up another chart representing what you know about the two robots working together.
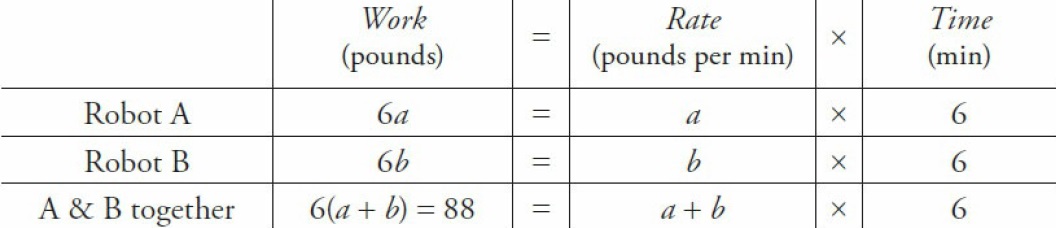
image1.jpg [ 50.99 KiB | Viewed 10389 times ]
Now, 6(a + b) = 88 and, from the question stem, robot A’s rate is \(\frac{3}{5}\) of B’s rate. This can be written as \(a = \frac{3}{5}b\). To solve for a, substitute for b:
\(a = \frac{3}{5} b\)
\(\frac{5}{3}a = b\)
\(6(a+ \frac{5}{3}a) = 88\)
\(6 \frac{8}{3} a = 88\)
\(a = \frac{11}{2}\)
So A’s rate is pounds per minute. Now just plug into the original chart:
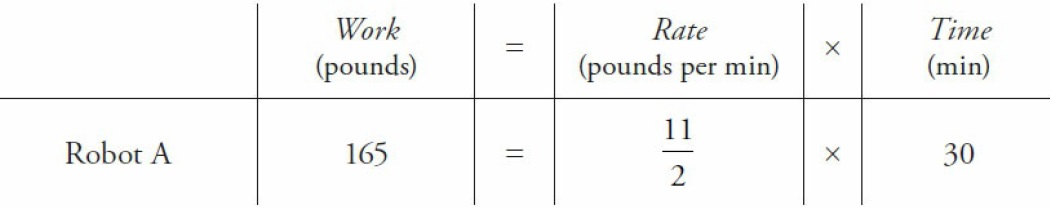
image1.jpg [ 28.05 KiB | Viewed 10380 times ]
The time robot A takes to polish 165 pounds of gems is \(165/\frac{11}{2} =\frac{330}{165} = 30\) minutes.
When rate problems involve multiple situations, it can help to set up an initial “skeleton” W= RT chart for the solution. That way, you can determine what data is needed and fill in that data as you find it. Since the question asks how long robot A will take alone, the chart will look like this:
Attachment:
image1.jpg [ 26.04 KiB | Viewed 10355 times ]
Work is known and the question asks for time, so robot A’s rate is needed. Call the rates a and b. Now set up another chart representing what you know about the two robots working together.
Attachment:
image1.jpg [ 50.99 KiB | Viewed 10389 times ]
Now, 6(a + b) = 88 and, from the question stem, robot A’s rate is \(\frac{3}{5}\) of B’s rate. This can be written as \(a = \frac{3}{5}b\). To solve for a, substitute for b:
\(a = \frac{3}{5} b\)
\(\frac{5}{3}a = b\)
\(6(a+ \frac{5}{3}a) = 88\)
\(6 \frac{8}{3} a = 88\)
\(a = \frac{11}{2}\)
So A’s rate is pounds per minute. Now just plug into the original chart:
Attachment:
image1.jpg [ 28.05 KiB | Viewed 10380 times ]
The time robot A takes to polish 165 pounds of gems is \(165/\frac{11}{2} =\frac{330}{165} = 30\) minutes.
