
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
The figure above shown
[#permalink]
 17 Feb 2017, 03:05
17 Feb 2017, 03:05
3
Expert Reply
3
Bookmarks
Question Stats:
 93% (00:43) correct
93% (00:43) correct
 6% (00:52) wrong
6% (00:52) wrong  based on 199 sessions
based on 199 sessions
Hide Show timer Statistics
Attachment:
#Grepracticequestion The figure above shows a regular 9-sides polygon.jpg [ 7.79 KiB | Viewed 45858 times ]
The figure above shows a regular 9-sides polygon. What is the value of X ?
Insert the value
Show: :: OA
40°
Re: The figure above shown
[#permalink]
 25 Feb 2017, 17:45
25 Feb 2017, 17:45
8
Expert Reply
Explanation
The sum of the interior angles of a polygon, use 180(n − 2), where n is the number of sides: Sum of the interior angles = 180(9 − 2) → 180(7) → 1260°.
Since this 9-sided figure is regular, all of the interior angles are equal: 1260° \(\div\) 9 = 140°.
Now we can find x:
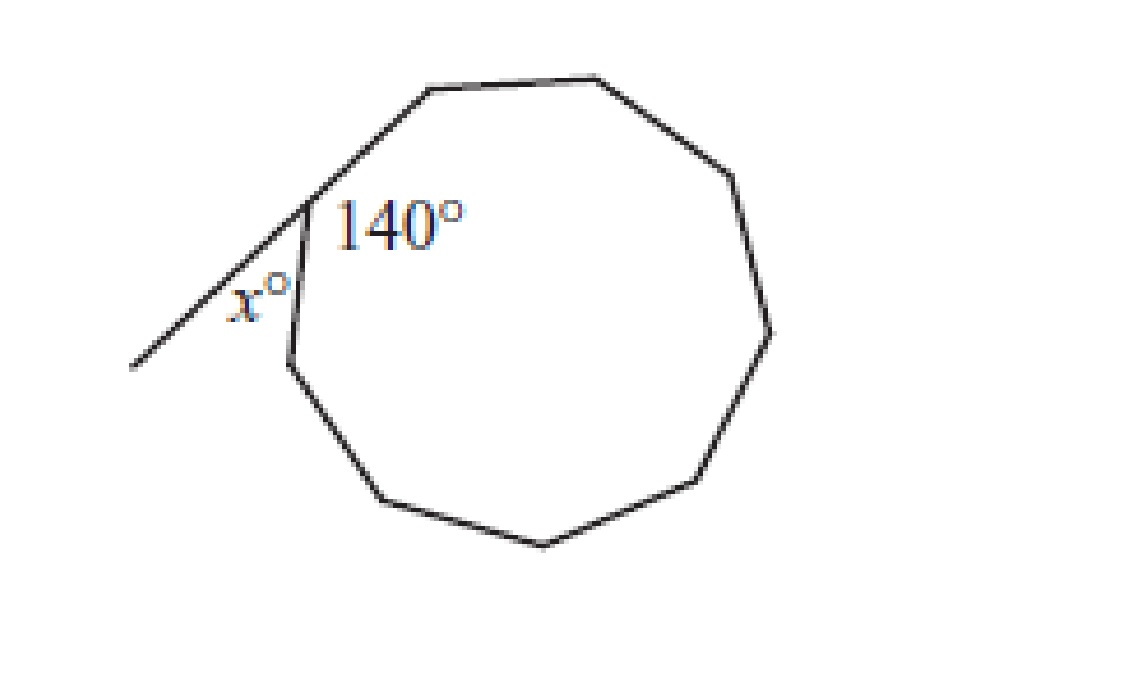
x° + 140° = 180°
x = 40°
Hence the value 40 is correct.
di new.jpg [ 39.94 KiB | Viewed 60289 times ]
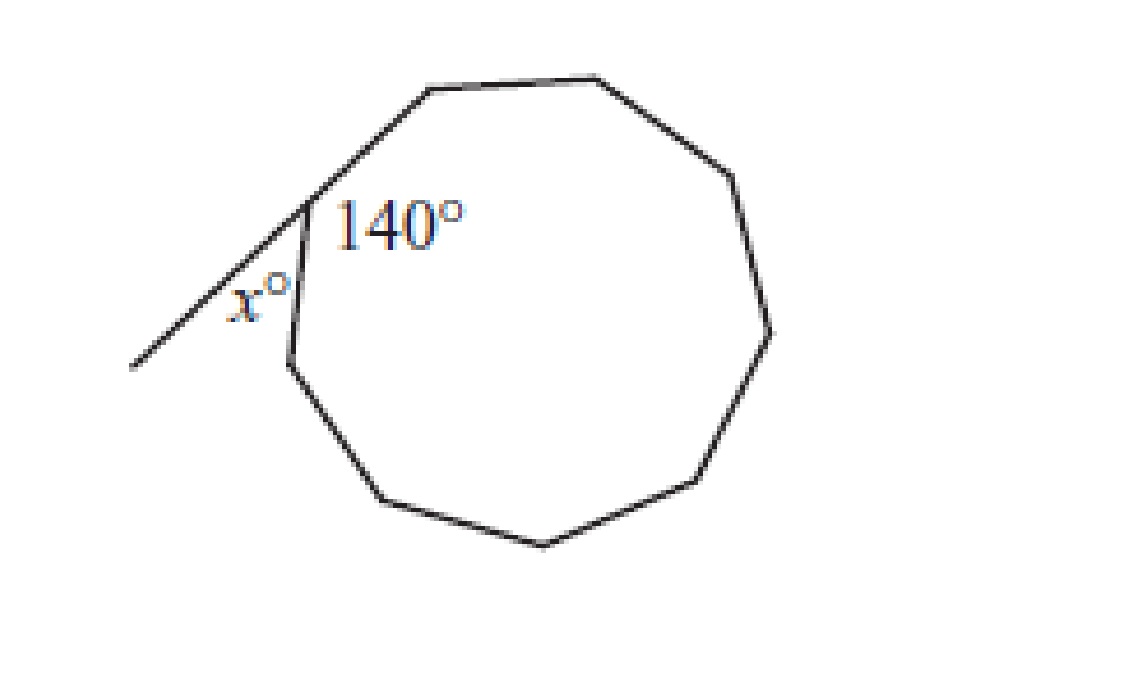
The sum of the interior angles of a polygon, use 180(n − 2), where n is the number of sides: Sum of the interior angles = 180(9 − 2) → 180(7) → 1260°.
Since this 9-sided figure is regular, all of the interior angles are equal: 1260° \(\div\) 9 = 140°.
Now we can find x:
x° + 140° = 180°
x = 40°
Hence the value 40 is correct.
Show: :: Img
Attachment:
di new.jpg [ 39.94 KiB | Viewed 60289 times ]
General Discussion
Re: The figure above shown
[#permalink]
 17 Feb 2017, 20:09
17 Feb 2017, 20:09
1
i think answer 15 is wrong. I found an answer 40











