
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If x and y are numbers on the number line above, which of the followin
[#permalink]
 16 Dec 2021, 03:10
16 Dec 2021, 03:10
Expert Reply
2
Bookmarks
Question Stats:
 64% (00:53) correct
64% (00:53) correct
 35% (00:48) wrong
35% (00:48) wrong  based on 39 sessions
based on 39 sessions
Hide Show timer Statistics
Note: Figure not drawn to scale
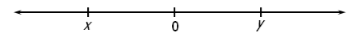
If x and y are numbers on the number line above, which of the following statements must be true?
I. |x+y| < y
II. x + y < 0
III. xy < 0
A. I only
B. III only
C. I and II
D. I and III
E. II and III
Kudos for a correct solution.
If x and y are numbers on the number line above, which of the following statements must be true?
I. |x+y| < y
II. x + y < 0
III. xy < 0
A. I only
B. III only
C. I and II
D. I and III
E. II and III
Kudos for a correct solution.
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: If x and y are numbers on the number line above, which of the followin
[#permalink]
 16 Dec 2021, 04:40
16 Dec 2021, 04:40
Carcass wrote:
Note: Figure not drawn to scale
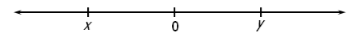
If x and y are numbers on the number line above, which of the following statements must be true?
I. |x+y| < y
II. x + y < 0
III. xy < 0
A. I only
B. III only
C. I and II
D. I and III
E. II and III
Kudos for a correct solution.
If x and y are numbers on the number line above, which of the following statements must be true?
I. |x+y| < y
II. x + y < 0
III. xy < 0
A. I only
B. III only
C. I and II
D. I and III
E. II and III
Kudos for a correct solution.
I. |x+y| < y
Statement I is not necessarily true.
For example, if x = -5 and y = 1, the inequality |x+y| < y becomes: |(-5) + 1| < 1, which simplifies to be: 4 < 1, which is not true.
This means we can eliminate answer choices A, D and D since they state that statement I is true.
II. x + y < 0
Statement II is not necessarily true.
For example, if x = -1 and y = 2, the inequality x + y < 0 becomes: (-1) + 2 < 0, which simplifies to be: 1 < 0, which is not true.
This means we can eliminate answer choice E since it states that statement II is true.
By the process of elimination, the correct answer is B
Moderator

Joined: 02 Jan 2020
Status:GRE Quant Tutor
Posts: 1141
Given Kudos: 9
Location: India
Concentration: General Management
Schools: XLRI Jamshedpur, India - Class of 2014
GMAT 1: 700 Q51 V31
GPA: 2.8
WE:Engineering (Computer Software)
If x and y are numbers on the number line above, which of the followin
[#permalink]
 30 Dec 2021, 20:55
30 Dec 2021, 20:55
1
It is given to us that x is negative and y is positive but we do not know the actual values of x and y
Since it is a must be true question so let's take values of x and y to prove the option choices wrong
I. |x+y| < y Now on LHS (Left Hand Side) we have |x+y| and RHS (Right Hand Side) we have y
So, we need to get a value of |x+y| which is bigger or equal to y in order to prove this wrong
Lets take a small negative value of x and small positive value of y
x = -100, y = 10
|x+y| = |-100+10| = |-90| = 90 > 10 (Watch this video to learn the Basics of Absolute Value)
=> |x+y| < y MUST not be true always
II. x + y < 0
x = -10, y = 100
x+y = 90 > 0
=> x + y < 0 MUST not be true always
III. xy < 0
x = -10, y = 100
or x = -100, y = 10
In any case xy < 0 (Watch this video to learn the Basics of Inequalities)
As product of a negative number and a positive number < 0
=> xy < 0 is Always True
So, Answer will be B
Hope it helps!
Watch the following video to learn the Basics of Absolute Values
Since it is a must be true question so let's take values of x and y to prove the option choices wrong
I. |x+y| < y Now on LHS (Left Hand Side) we have |x+y| and RHS (Right Hand Side) we have y
So, we need to get a value of |x+y| which is bigger or equal to y in order to prove this wrong
Lets take a small negative value of x and small positive value of y
x = -100, y = 10
|x+y| = |-100+10| = |-90| = 90 > 10 (Watch this video to learn the Basics of Absolute Value)
=> |x+y| < y MUST not be true always
II. x + y < 0
x = -10, y = 100
x+y = 90 > 0
=> x + y < 0 MUST not be true always
III. xy < 0
x = -10, y = 100
or x = -100, y = 10
In any case xy < 0 (Watch this video to learn the Basics of Inequalities)
As product of a negative number and a positive number < 0
=> xy < 0 is Always True
So, Answer will be B
Hope it helps!
Watch the following video to learn the Basics of Absolute Values





