
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If |-2 - x| < 5, which of the following is a possible value of x? PU
[#permalink]
 28 Feb 2022, 05:00
28 Feb 2022, 05:00
Expert Reply
1
Bookmarks
Question Stats:
 65% (01:07) correct
65% (01:07) correct
 35% (00:52) wrong
35% (00:52) wrong  based on 20 sessions
based on 20 sessions
Hide Show timer Statistics
If \(|-2 - x| < 5\), which of the following is a possible value of x?
(A) -7
(B) -5
(C) 3
(D) 5
(E) 7
(A) -7
(B) -5
(C) 3
(D) 5
(E) 7
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: If |-2 - x| < 5, which of the following is a possible value of x? PU
[#permalink]
 28 Feb 2022, 05:35
28 Feb 2022, 05:35
1
Carcass wrote:
If \(|-2 - x| < 5\), which of the following is a possible value of x?
(A) -7
(B) -5
(C) 3
(D) 5
(E) 7
(A) -7
(B) -5
(C) 3
(D) 5
(E) 7
STRATEGY: As with all GRE Multiple Choice questions, we should immediately ask ourselves, Can I use the answer choices to my advantage?
In this case, we can easily test each answer choice to see which one satisfies the given inequality.
That's said, the algebraic solution is pretty fast as well.
So let's use some algebra
----ASIDE----------------
When solving inequalities involving ABSOLUTE VALUE, there are 2 things you need to know:
Rule #1: If |something| < k, then –k < something < k
Rule #2: If |something| > k, then EITHER something > k OR something < -k
Note: these rules assume that k is positive
------------------------------
Given: |-2 - x| < 5 [Notice that this inequality is in the same form as Rule #1]
So, we can write: -5 < -2 - x < 5
Add 2 to all sides of the inequality: -3 < -x < 7
Multiply all sides of the inequality by -1 to get: 3 > x > -7 [Since I multiplied the inequality by a negative value I had to reverse the direction of the inequality symbol. For more on this, see the video below.]
Check the answer choices.... the only option that satisfies the resulting inequality is -5.
Answer: B
RELATED VIDEO
Moderator

Joined: 02 Jan 2020
Status:GRE Quant Tutor
Posts: 1141
Given Kudos: 9
Location: India
Concentration: General Management
Schools: XLRI Jamshedpur, India - Class of 2014
GMAT 1: 700 Q51 V31
GPA: 2.8
WE:Engineering (Computer Software)
Re: If |-2 - x| < 5, which of the following is a possible value of x? PU
[#permalink]
 26 Aug 2022, 08:49
26 Aug 2022, 08:49
1
Given that \(|-2 - x| < 5\) and we need to find which of the option choices is a possible value of x
Let's solve the problem using two methods
Method 1: Substitution
We will values in each option choice and plug in the question and check if it satisfies the question or not.
(A) -7
Lets take x = -7 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - (-7)| < 5\)
=> |5| < 5
=> 5 < 5 which is FALSE
(B) -5
Lets take x = -5 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - (-5)| < 5\)
=> |3| < 5
=> 3 < 5 which is TRUE
In test situation we DONT need to proceed further, but I am solving for all option choice to complete the solution.
(C) 3
Lets take x = 3 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - 3| < 5\)
=> |-5| < 5
=> 5 < 5 which is FALSE
(D) 5
Lets take x = 5 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - 5| < 5\)
=> |-7| < 5
=> 7 < 5 which is FALSE
(E) 7
Lets take x = 7 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - 7| < 5\)
=> |-9| < 5
=> 9 < 5 which is FALSE
So, Answer will be B
Method 2: Algebra
Now, we know that |A| < B can be opened as (Watch this video to know about the Basics of Absolute Value)
A < B for A ≥ 0 and
-A < B for A < 0
=> |-2 - x| < 5 can be written as
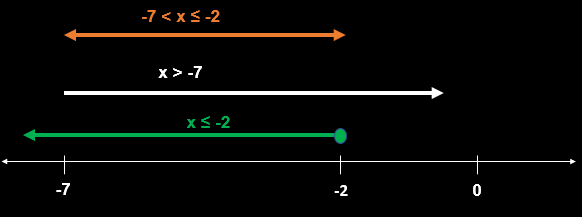
Case 1: -2 - x ≥ 0 or x ≤ -2
=> -2 - x < 5
=> x > -2 -5
=> x > -7
And the condition was x ≤ -2, so the solution will be part common between x ≤ -2 and and x > -7
=> -7 < x ≤ -2 is a solution ...(1)
-7 to -2.PNG [ 3.32 KiB | Viewed 1835 times ]
x = -5 lies in this range so We can mark B as answer and move on in the test. but I am solving for all option choice to complete the solution
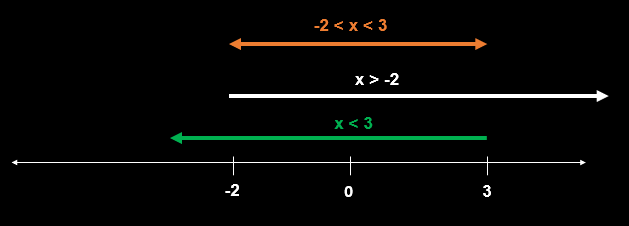
Case 2: -2 - x < 0 or x > -2
=> -(-2 - x) < 5
=> 2 + x < 5
=> x < 5-2
=> x < 3
And the condition was x > -2, so the solution will be part common between x > -2 and and x < 3
=> -2 < x < 3 is a solution ...(2)
-2 to 3.PNG [ 3.08 KiB | Viewed 1862 times ]
So, final solution will be a combination of (1) and (2)
=> -7 < x ≤ -2 and -2 < x < 3
=> -7 < x < 3
So, Answer will be B
Hope it helps!
Watch the following video to learn How to Solve Absolute Value Problems
Let's solve the problem using two methods
Method 1: Substitution
We will values in each option choice and plug in the question and check if it satisfies the question or not.
(A) -7
Lets take x = -7 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - (-7)| < 5\)
=> |5| < 5
=> 5 < 5 which is FALSE
(B) -5
Lets take x = -5 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - (-5)| < 5\)
=> |3| < 5
=> 3 < 5 which is TRUE
In test situation we DONT need to proceed further, but I am solving for all option choice to complete the solution.
(C) 3
Lets take x = 3 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - 3| < 5\)
=> |-5| < 5
=> 5 < 5 which is FALSE
(D) 5
Lets take x = 5 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - 5| < 5\)
=> |-7| < 5
=> 7 < 5 which is FALSE
(E) 7
Lets take x = 7 and substitute in \(|-2 - x| < 5\) and see if satisfies the equation
=> \(|-2 - 7| < 5\)
=> |-9| < 5
=> 9 < 5 which is FALSE
So, Answer will be B
Method 2: Algebra
Now, we know that |A| < B can be opened as (Watch this video to know about the Basics of Absolute Value)
A < B for A ≥ 0 and
-A < B for A < 0
=> |-2 - x| < 5 can be written as
Case 1: -2 - x ≥ 0 or x ≤ -2
=> -2 - x < 5
=> x > -2 -5
=> x > -7
And the condition was x ≤ -2, so the solution will be part common between x ≤ -2 and and x > -7
=> -7 < x ≤ -2 is a solution ...(1)
Attachment:
-7 to -2.PNG [ 3.32 KiB | Viewed 1835 times ]
x = -5 lies in this range so We can mark B as answer and move on in the test. but I am solving for all option choice to complete the solution
Case 2: -2 - x < 0 or x > -2
=> -(-2 - x) < 5
=> 2 + x < 5
=> x < 5-2
=> x < 3
And the condition was x > -2, so the solution will be part common between x > -2 and and x < 3
=> -2 < x < 3 is a solution ...(2)
Attachment:
-2 to 3.PNG [ 3.08 KiB | Viewed 1862 times ]
So, final solution will be a combination of (1) and (2)
=> -7 < x ≤ -2 and -2 < x < 3
=> -7 < x < 3
So, Answer will be B
Hope it helps!
Watch the following video to learn How to Solve Absolute Value Problems





