
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
How many integer values of p are there such that |p - 3| < 4/3?
[#permalink]
 07 Apr 2022, 05:41
07 Apr 2022, 05:41
Expert Reply
1
Bookmarks
Question Stats:
 40% (01:32) correct
40% (01:32) correct
 59% (01:31) wrong
59% (01:31) wrong  based on 49 sessions
based on 49 sessions
Hide Show timer Statistics
How many integer values of p are there such that |p - 3| < 4/3?
A. 0
B. 1
C. 2
D. 3
E. 4
A. 0
B. 1
C. 2
D. 3
E. 4
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: How many integer values of p are there such that |p - 3| < 4/3?
[#permalink]
 07 Apr 2022, 05:51
07 Apr 2022, 05:51
Carcass wrote:
How many integer values of p are there such that |p - 3| < 4/3?
A. 0
B. 1
C. 2
D. 3
E. 4
A. 0
B. 1
C. 2
D. 3
E. 4
Two properties involving absolute value inequalities:
Property #1: If |something| < k, then –k < something < k
Property #2: If |something| > k, then EITHER something > k OR something < -k
Note: these rules assume that k is positive
Since the given equation is in the same form as property #1, we can write: -4/3 < p - 3 < 4/3
To provide a clear picture, let's express the fractions as decimal approximations: -1.33 < p - 3 < 1.33
Now add 3 to all parts of the inequality: 1.67 < p < 4.33
Since p is an integer, there are three possible values of p that satisfied the inequality 1.67 < p < 4.33.
The values are p = 2, p = 3, and p = 4
Answer: D
Moderator

Joined: 02 Jan 2020
Status:GRE Quant Tutor
Posts: 1141
Given Kudos: 9
Location: India
Concentration: General Management
Schools: XLRI Jamshedpur, India - Class of 2014
GMAT 1: 700 Q51 V31
GPA: 2.8
WE:Engineering (Computer Software)
How many integer values of p are there such that |p - 3| < 4/3?
[#permalink]
 29 May 2022, 08:41
29 May 2022, 08:41
Given that |p - 3| < \(\frac{4}{3}\) and we need to find how many integer values of p satisfy this equation
To open |p - 3| we need to take two cases (Watch this video to know about the Basics of Absolute Value)
Case 1: Assume that whatever is inside the Absolute Value/Modulus is non-negative
=> p - 3 ≥ 0 => p ≥ 3
|p - 3| = p - 3 (as if A ≥ 0 then |A| = A)
=> p - 3 < \(\frac{4}{3}\)
=> p < \(\frac{4}{3}\) + 3
=> p < \(\frac{4+3*3}{3}\)
=> p < \(\frac{13}{3}\) ~ 4.33
=> But our condition was p ≥ 3. So solution will be the range common in both of them (refer below image)
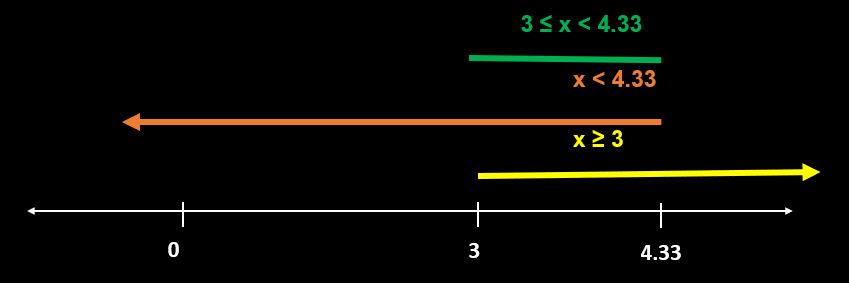
temp3 to 4.33.JPG [ 22.07 KiB | Viewed 2534 times ]
=> 3 ≤ p < 4.33
So, possible integer values of p in this range are 3 and 4
Case 2: Assume that whatever is inside the Absolute Value/Modulus is Negative
p - 3 < 0 => p < 3
|p - 3| < \(\frac{4}{3}\) (as if A < 0 then |A| = -A)
=> -(p - 3) < \(\frac{4}{3}\)
=> -p + 3 < \(\frac{4}{3}\)
=> p > 3 - \(\frac{4}{3}\)
=> p > \(\frac{3*3 - 4}{3}\)
=> p > \(\frac{5}{3}\) ~ 1.67
=> But our condition was p < 3. So solution will be the range common in both of them (refer below image)
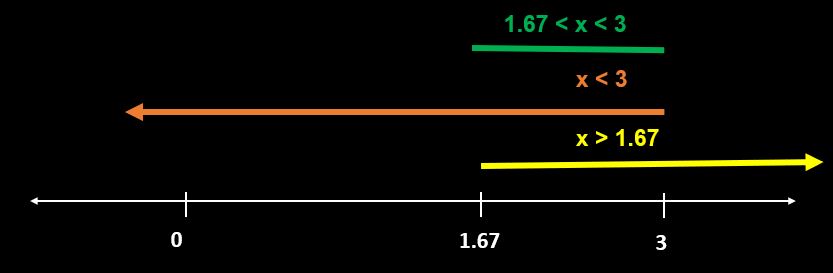
1.67 to 3.JPG [ 21.76 KiB | Viewed 2529 times ]
=> 1.67 < p < 3
So, possible integer values of p in this range is 2
=> Final values of p are 2, 3, 4 => 3 values
So, Answer will be D
Hope it helps!
Watch the following video to learn How to Solve Absolute Value Problems
To open |p - 3| we need to take two cases (Watch this video to know about the Basics of Absolute Value)
Case 1: Assume that whatever is inside the Absolute Value/Modulus is non-negative
=> p - 3 ≥ 0 => p ≥ 3
|p - 3| = p - 3 (as if A ≥ 0 then |A| = A)
=> p - 3 < \(\frac{4}{3}\)
=> p < \(\frac{4}{3}\) + 3
=> p < \(\frac{4+3*3}{3}\)
=> p < \(\frac{13}{3}\) ~ 4.33
=> But our condition was p ≥ 3. So solution will be the range common in both of them (refer below image)
Attachment:
temp3 to 4.33.JPG [ 22.07 KiB | Viewed 2534 times ]
=> 3 ≤ p < 4.33
So, possible integer values of p in this range are 3 and 4
Case 2: Assume that whatever is inside the Absolute Value/Modulus is Negative
p - 3 < 0 => p < 3
|p - 3| < \(\frac{4}{3}\) (as if A < 0 then |A| = -A)
=> -(p - 3) < \(\frac{4}{3}\)
=> -p + 3 < \(\frac{4}{3}\)
=> p > 3 - \(\frac{4}{3}\)
=> p > \(\frac{3*3 - 4}{3}\)
=> p > \(\frac{5}{3}\) ~ 1.67
=> But our condition was p < 3. So solution will be the range common in both of them (refer below image)
Attachment:
1.67 to 3.JPG [ 21.76 KiB | Viewed 2529 times ]
=> 1.67 < p < 3
So, possible integer values of p in this range is 2
=> Final values of p are 2, 3, 4 => 3 values
So, Answer will be D
Hope it helps!
Watch the following video to learn How to Solve Absolute Value Problems





