
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Circle K has a total area of 9pi. Circle M has a total area
[#permalink]
 30 Sep 2019, 15:36
30 Sep 2019, 15:36
Expert Reply
Question Stats:
 92% (00:37) correct
92% (00:37) correct
 7% (00:48) wrong
7% (00:48) wrong  based on 13 sessions
based on 13 sessions
Hide Show timer Statistics
Circle K has a total area of \(9\pi\). Circle M has a total area of \(49\pi\). Suppose the circles intersect at exactly one point. Which of the following could be the distance from the center for Circle K to the center of Circle M?
A. 8
B. 21
C. 10
D. 29
E. 58
Kudos for the right answer and explanation
A. 8
B. 21
C. 10
D. 29
E. 58
Kudos for the right answer and explanation
Moderator

Joined: 02 Jan 2020
Status:GRE Quant Tutor
Posts: 1141
Given Kudos: 9
Location: India
Concentration: General Management
Schools: XLRI Jamshedpur, India - Class of 2014
GMAT 1: 700 Q51 V31
GPA: 2.8
WE:Engineering (Computer Software)
Circle K has a total area of 9pi. Circle M has a total area
[#permalink]
 07 Jun 2020, 01:10
07 Jun 2020, 01:10
[Refer attached figure]
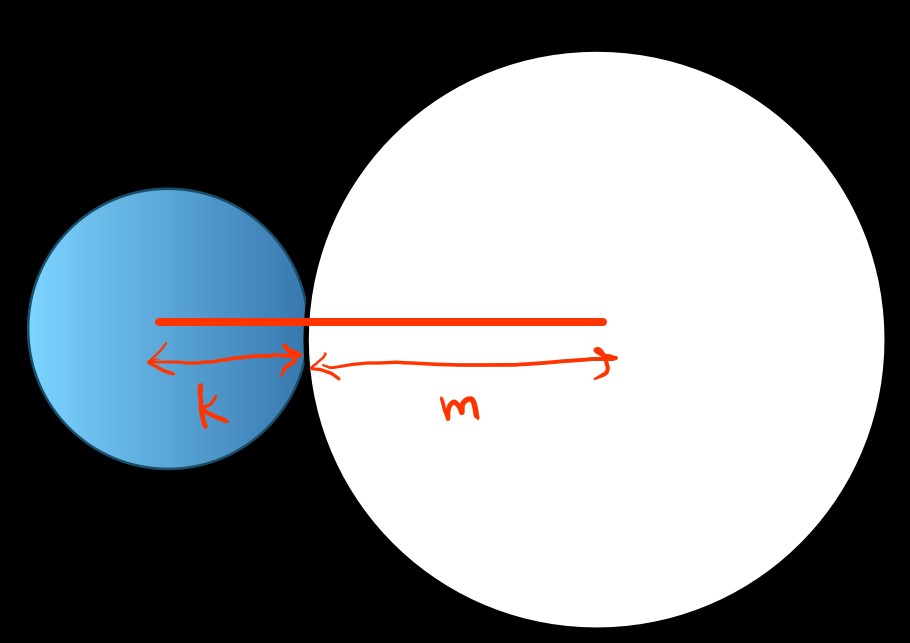
image-1.jpg [ 59.97 KiB | Viewed 1495 times ]
Since the two circles are intersecting only at one point then it means that the distance between their centers = sum of their radius
Note that if two circles intersect at more than two points then distance between their centers will be less than sum of their radius
=> Distance from the center for Circle K to the center of Circle M = Radius of Circle K + Radius of Circle M = k + m [where k and m are radius of circle M and K respectively]
Circle K has a total area of \(9\pi\) = \(\pi\)\(k^2\) [We know that area of Circle with radius r is \(9\pi\)]
=> \(k^2\) = 9 => k = 3
Circle M has a total area of \(49\pi\) = \(\pi\)\(m^2\) [We know that area of Circle with radius r is \(9\pi\)]
=> \(m^2\) = 49 => m = 7
Distance from the center for Circle K to the center of Circle M = k + m = 3 + 7 = 10
So, answer will be C
Hope it helps!
Watch the following video to Learn Basics of Circles
Attachment:
image-1.jpg [ 59.97 KiB | Viewed 1495 times ]
Since the two circles are intersecting only at one point then it means that the distance between their centers = sum of their radius
Note that if two circles intersect at more than two points then distance between their centers will be less than sum of their radius
=> Distance from the center for Circle K to the center of Circle M = Radius of Circle K + Radius of Circle M = k + m [where k and m are radius of circle M and K respectively]
Circle K has a total area of \(9\pi\) = \(\pi\)\(k^2\) [We know that area of Circle with radius r is \(9\pi\)]
=> \(k^2\) = 9 => k = 3
Circle M has a total area of \(49\pi\) = \(\pi\)\(m^2\) [We know that area of Circle with radius r is \(9\pi\)]
=> \(m^2\) = 49 => m = 7
Distance from the center for Circle K to the center of Circle M = k + m = 3 + 7 = 10
So, answer will be C
Hope it helps!
Watch the following video to Learn Basics of Circles

gmatclubot
Circle K has a total area of 9pi. Circle M has a total area [#permalink]
07 Jun 2020, 01:10
Moderators:



