GeminiHeat wrote:
A circle is inscribed within a regular hexagon in such a way that the circle touches all sides of the hexagon at exactly one point per side. Another circle is drawn to connect all the vertices of the hexagon. Expressed as a fraction, what is the ratio of the area of the smaller circle to the area of the larger circle?
A. √(2/3)
B. (√2)/3
C. (√3)/2
D. (√3)/4
E. 3/4
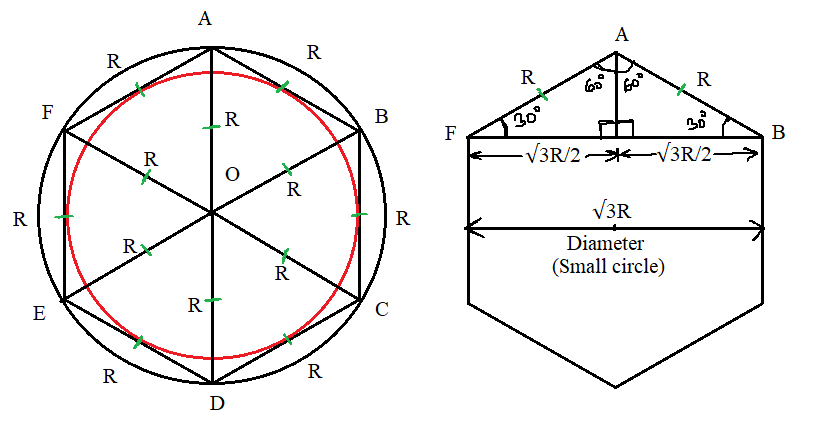
Let the radius of larger circle be \(R\)
We know, a regular hexagon gets divided into 6 equilateral triangle when all of its vertices are joined with its centre.
Refer to the figure below;
In regular hexagon ABCDEEF, AB = BC = CD = DE = EF = FA = \(R\)
Now in isosceles triangle ABF, AB = AF = \(R\) and BF = \(\sqrt{3}R\)
Also notice that BF is the diameter of the smaller circle
Therefore, radius of the smaller circle = \(\frac{\sqrt{3}R}{2}\)
Ratio of the areas = \((\frac{\sqrt{3}}{2})^2 = \frac{3}{4}\)
Hence, option E
Attachments
A circle is inscribed within a regular hexagon.png [ 23.04 KiB | Viewed 2349 times ]









 44% (02:28) correct
44% (02:28) correct


