
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If |x + 1 | > 2x - 1, which of the following represents the correct ra
[#permalink]
 29 Jun 2022, 09:04
29 Jun 2022, 09:04
Expert Reply
2
Bookmarks
Question Stats:
 45% (01:16) correct
45% (01:16) correct
 55% (01:41) wrong
55% (01:41) wrong  based on 20 sessions
based on 20 sessions
Hide Show timer Statistics
If |x + 1 | > 2x - 1, which of the following represents the correct range of values of x ?
A. x < 0
B. x < 2
C. -2 < x < 0
D. -1 < x < 2
E. 0 < x < 2
A. x < 0
B. x < 2
C. -2 < x < 0
D. -1 < x < 2
E. 0 < x < 2
Part of the project: GRE QCQ & PS 3 Questions Every One DAILY Challenge - (2022)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
GRE Math Essentials for a TOP Quant Score - Q170!!! (2021)
GRE Geometry Formulas for a Q170
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
GRE Math Essentials for a TOP Quant Score - Q170!!! (2021)
GRE Geometry Formulas for a Q170
GRE - Math Book
Moderator

Joined: 02 Jan 2020
Status:GRE Quant Tutor
Posts: 1141
Given Kudos: 9
Location: India
Concentration: General Management
Schools: XLRI Jamshedpur, India - Class of 2014
GMAT 1: 700 Q51 V31
GPA: 2.8
WE:Engineering (Computer Software)
Re: If |x + 1 | > 2x - 1, which of the following represents the correct ra
[#permalink]
 25 Aug 2022, 10:48
25 Aug 2022, 10:48
Given that |x + 1 | > 2x - 1 and we need to find the correct range of values of x
Let's solve the problem using two methods
Method 1: Substitution
We will values in each option choice and plug in the question and check if it satisfies the question or not. ( Idea is to take such values which can prove the question wrong)
A. x < 0
Lets take x = -1 (which falls in this range of x < 0) and substitute in the equation |x + 1 | > 2x - 1
=> |-1 + 1 | > 2*-1 - 1
=> | 0| > -3
=> 0 > -3 which is TRUE, but let's see if we can find a bigger range
B. x < 2
Lets take x = 1.9 (which falls in this range of x < 2) and substitute in the equation |x + 1 | > 2x - 1
=> |1.9 + 1 | > 2*1.9 - 1
=> | 2.9 | > 2.8
=> 0 > -3 which is TRUE.
Now, this range is bigger than option A, so we can ignore option A now.
C. -2 < x < 0
This is a subset of Option B so we don't need to check this one
D. -1 < x < 2
This is a subset of Option B so we don't need to check this one
E. 0 < x < 2
This is a subset of Option B so we don't need to check this one
So, Answer will be B
Method 2: Algebra
Now, we know that |A| > B can be opened as (Watch this video to know about the Basics of Absolute Value)
A > B for A ≥ 0 and
-A > B for A < 0
=> |x + 1 | > 2x - 1 can be written as
Case 1: x + 1 ≥ 0 or x ≥ -1
=> x + 1 > 2x - 1
=> 2x - x < 1 + 1
=> x < 2
And the condition was x ≥ -1 and we got the answer as x < 2
=> the solution will be the range common in both of them
=> -1 ≤ x < 2
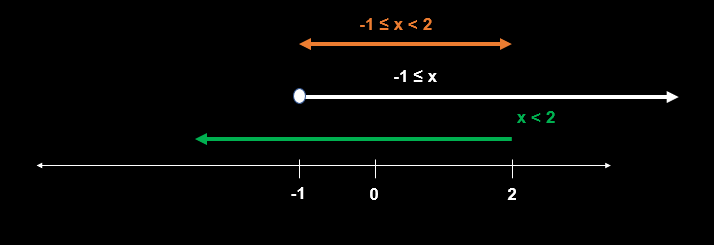
-1 to 2.PNG [ 3.5 KiB | Viewed 1883 times ]
Case 2: x + 1 < 0 or x < -1
=> -(x + 1) > 2x - 1
=> 2x + x < 1 - 1
=> 3x < 0
=> x < 0
And the condition was x < -1 and we got the answer as x < 0
=> the solution will be the range common in both of them
=> x < -1
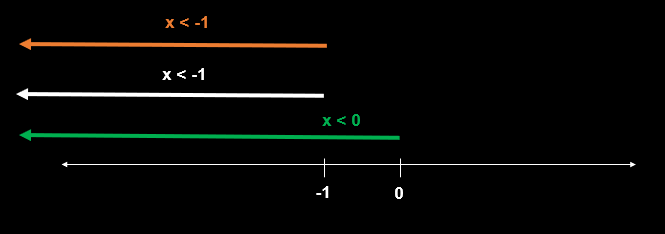
less than -1.PNG [ 3.54 KiB | Viewed 1917 times ]
Combining both the cases we get the answer as -1 ≤ x < 2 and x < -1
=> x < 2
So, Answer will be B
Hope it helps!
Watch the following video to learn How to Solve Absolute Value Problems
Let's solve the problem using two methods
Method 1: Substitution
We will values in each option choice and plug in the question and check if it satisfies the question or not. ( Idea is to take such values which can prove the question wrong)
A. x < 0
Lets take x = -1 (which falls in this range of x < 0) and substitute in the equation |x + 1 | > 2x - 1
=> |-1 + 1 | > 2*-1 - 1
=> | 0| > -3
=> 0 > -3 which is TRUE, but let's see if we can find a bigger range
B. x < 2
Lets take x = 1.9 (which falls in this range of x < 2) and substitute in the equation |x + 1 | > 2x - 1
=> |1.9 + 1 | > 2*1.9 - 1
=> | 2.9 | > 2.8
=> 0 > -3 which is TRUE.
Now, this range is bigger than option A, so we can ignore option A now.
C. -2 < x < 0
This is a subset of Option B so we don't need to check this one
D. -1 < x < 2
This is a subset of Option B so we don't need to check this one
E. 0 < x < 2
This is a subset of Option B so we don't need to check this one
So, Answer will be B
Method 2: Algebra
Now, we know that |A| > B can be opened as (Watch this video to know about the Basics of Absolute Value)
A > B for A ≥ 0 and
-A > B for A < 0
=> |x + 1 | > 2x - 1 can be written as
Case 1: x + 1 ≥ 0 or x ≥ -1
=> x + 1 > 2x - 1
=> 2x - x < 1 + 1
=> x < 2
And the condition was x ≥ -1 and we got the answer as x < 2
=> the solution will be the range common in both of them
=> -1 ≤ x < 2
Attachment:
-1 to 2.PNG [ 3.5 KiB | Viewed 1883 times ]
Case 2: x + 1 < 0 or x < -1
=> -(x + 1) > 2x - 1
=> 2x + x < 1 - 1
=> 3x < 0
=> x < 0
And the condition was x < -1 and we got the answer as x < 0
=> the solution will be the range common in both of them
=> x < -1
Attachment:
less than -1.PNG [ 3.54 KiB | Viewed 1917 times ]
Combining both the cases we get the answer as -1 ≤ x < 2 and x < -1
=> x < 2
So, Answer will be B
Hope it helps!
Watch the following video to learn How to Solve Absolute Value Problems
General Discussion
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: If |x + 1 | > 2x - 1, which of the following represents the correct ra
[#permalink]
 29 Jun 2022, 09:22
29 Jun 2022, 09:22
Carcass wrote:
If |x + 1 | > 2x - 1, which of the following represents the correct range of values of x ?
A. x < 0
B. x < 2
C. -2 < x < 0
D. -1 < x < 2
E. 0 < x < 2
A. x < 0
B. x < 2
C. -2 < x < 0
D. -1 < x < 2
E. 0 < x < 2
I find that the quickest solutions to this kind of question involve testing the answer choices
Scan the answer choices
Notice that some answer choices say that x = 1 is a solution and some say x = 1 is NOT a solution.
So, let's test x = 1
Plug it into the original inequality to get: |1 + 1 | > 2(1) - 1
Simplify to get: 2 > 1
Perfect!
So, x = 1 IS a solution to the inequality.
Since answer choices A and C do NOT include x = 1 as a solution, we can ELIMINATE them.
Now scan the remaining answer choices (B, D and E)
Some answer choices say that x = -1 is a solution and some say x = -1 is NOT a solution.
So, let's test x = -1
Plug it into the original inequality to get: |(-1) + 1 | > 2(-1) - 1
Simplify to get: 0 > -3
Perfect!
So, x = -1 IS a solution to the inequality.
Since answer choices D and E do NOT include x = -1 as a solution, we can ELIMINATE them.
We're left with B
Answer: B
Cheers,
Brent




