
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If A, B and C represent different digits in the multiplicati
[#permalink]
 30 Jun 2018, 10:00
30 Jun 2018, 10:00
3
4
Bookmarks
Question Stats:
 57% (03:35) correct
57% (03:35) correct
 42% (01:37) wrong
42% (01:37) wrong  based on 38 sessions
based on 38 sessions
Hide Show timer Statistics
If A, B and C represent different digits in the multiplication, then A + B + C =
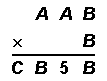
multiplication.png [ 905 Bytes | Viewed 17227 times ]
A 9
B 12
C 14
D 15
E 17
Attachment:
multiplication.png [ 905 Bytes | Viewed 17227 times ]
A 9
B 12
C 14
D 15
E 17
Re: If A, B and C represent different digits in the multiplicati
[#permalink]
 02 Jul 2018, 07:08
02 Jul 2018, 07:08
6
anuppatel012 wrote:
Please do share the shortcut if you have as solution...thanks
It is a step by step process,
First we have to calculate for Unit's digit B
We need a number that is B*B = B
So let us start as follows:
STEP 1
a) 0∗0=0 But entire answer will become zero
b) 1∗1=1 but the product will remain as AAB
c) 5∗5=25 but that won't be possible as (5 * A) + 2 = 7 , but we need 5
d) 6∗6=36 and 6∗A+3=5, so this value is Possible when A is 2 or A is 7
no other possible solution, so B is 6 and A is 2 or 7
STEP II
The product is AA6∗6=C656
Now if A is 2, it becomes 226∗6=1356 ; but we need C656
so if A is 7
776∗6=4656 which is = CB5B
Hence A+B+C=7+6+4=17
General Discussion
Re: If A, B and C represent different digits in the multiplicati
[#permalink]
 01 Jul 2018, 12:39
01 Jul 2018, 12:39
it is E...had to spend a lot of time figuring it out...took 335, 551, 553, 445, 776...atlast 776 worked 








