GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A painter paints the four equilaterally triangular regions adjoining
[#permalink]
06 May 2025, 02:16
06 May 2025, 02:16
Expert Reply
00:00
Question Stats:
50% (01:54) correct
50% (01:13) wrong based on 2 sessions
Hide Show timer Statistics
A painter paints the four equilaterally triangular regions adjoining the sides of a square $\(A B C D\)$ of diagonal $\(10 \sqrt{2}\)$. What is the ratio of the shaded region to the unshaded region?
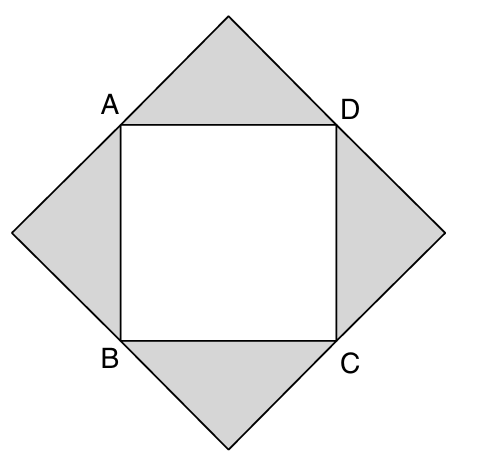
GRE figure geometry.png [ 8.44 KiB | Viewed 235 times ]
(A) $\(\sqrt{3}: 2\)$
(B) $\(\sqrt{3}: 1\)$
(C) $\(2: 1\)$
(D) $\(\sqrt{5}: 1\)$
(E) $\(\sqrt{5}: 2\)$
Attachment:
GRE figure geometry.png [ 8.44 KiB | Viewed 235 times ]
(A) $\(\sqrt{3}: 2\)$
(B) $\(\sqrt{3}: 1\)$
(C) $\(2: 1\)$
(D) $\(\sqrt{5}: 1\)$
(E) $\(\sqrt{5}: 2\)$
- Part of the project: GRE - Skill Builder Project II Edition - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
- Also replying to the unanswered questions
Re: A painter paints the four equilaterally triangular regions adjoining
[#permalink]
31 May 2025, 00:57
31 May 2025, 00:57
Expert Reply
\(\begin{aligned}
&\text { Since the diagonal of the square }=10 \sqrt{2} \Rightarrow \text { Side }=10\\
&\text { Shaded region }=4 \cdot\left(\frac{\sqrt{3}}{4} S^2\right)=4 \times \frac{1}{4} \times \sqrt{3} \times 10^2=10^2 \cdot \sqrt{3}
\end{aligned}\)
The area of un-shaded region $\(=10^2\)$
Therefore, the ratio of shaded to un-shaded region $\(=\sqrt{3}: 1\)$.
Thus, the correct answer is $B$.
&\text { Since the diagonal of the square }=10 \sqrt{2} \Rightarrow \text { Side }=10\\
&\text { Shaded region }=4 \cdot\left(\frac{\sqrt{3}}{4} S^2\right)=4 \times \frac{1}{4} \times \sqrt{3} \times 10^2=10^2 \cdot \sqrt{3}
\end{aligned}\)
The area of un-shaded region $\(=10^2\)$
Therefore, the ratio of shaded to un-shaded region $\(=\sqrt{3}: 1\)$.
Thus, the correct answer is $B$.
gmatclubot
Re: A painter paints the four equilaterally triangular regions adjoining [#permalink]
31 May 2025, 00:57
Moderators:
