
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A survey of 550 male managers and 650 female managers was c
[#permalink]
 18 Dec 2017, 12:35
18 Dec 2017, 12:35
1
1
Expert Reply
Question Stats:
 76% (05:14) correct
76% (05:14) correct
 23% (04:34) wrong
23% (04:34) wrong  based on 13 sessions
based on 13 sessions
Hide Show timer Statistics
A survey of 550 male managers and 650 female managers was conducted. All 1,200 managers identified whether, for each of six characteristics, the characteristic is important to consider when hiring a new employee. For each of the six characteristics, the percent of managers surveyed who identified that characteristic as important to consider is given in the following table.
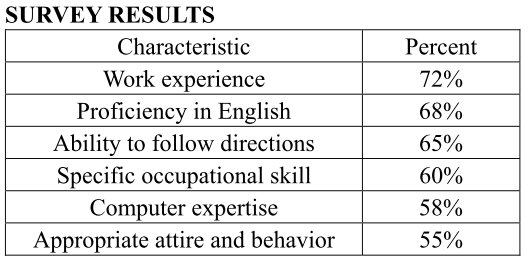
survey.jpg [ 74.47 KiB | Viewed 16586 times ]
Attachment:
survey.jpg [ 74.47 KiB | Viewed 16586 times ]
Which of the following statements about the managers surveyed must be true?
A. Less than 55 percent were male managers.
B. Of the male managers, more identified work experience as an important characteristic to consider than identified proficiency in English.
C. Less than 60 percent of the male managers identified specific occupational skill as important to consider.
The number of managers surveyed who identified work experience as an important characteristic to consider was approximately what percent greater than the number who identified appropriate attire and behavior as an important characteristic to consider?
A. 15%
B. 20%
C. 25%
D. 30%
E. 35%
If 48 percent of the managers surveyed identified both ability to follow directions and computer expertise as an important characteristics to consider, what percent of the managers surveyed identified neither of these characteristics as important to consider?
A. 15%
B. 18%
C. 23%
D. 25%
E. 28%
A. Less than 55 percent were male managers.
B. Of the male managers, more identified work experience as an important characteristic to consider than identified proficiency in English.
C. Less than 60 percent of the male managers identified specific occupational skill as important to consider.
Show: :: OA
A
The number of managers surveyed who identified work experience as an important characteristic to consider was approximately what percent greater than the number who identified appropriate attire and behavior as an important characteristic to consider?
A. 15%
B. 20%
C. 25%
D. 30%
E. 35%
Show: :: OA
D
If 48 percent of the managers surveyed identified both ability to follow directions and computer expertise as an important characteristics to consider, what percent of the managers surveyed identified neither of these characteristics as important to consider?
A. 15%
B. 18%
C. 23%
D. 25%
E. 28%
Show: :: OA
D
Sherpa Prep Representative
Joined: 15 Jan 2018
Posts: 147
Given Kudos: 0
Re: A survey of 550 male managers and 650 female managers was c
[#permalink]
 30 Jan 2018, 21:16
30 Jan 2018, 21:16
3
Expert Reply
Always spend a minute to read the chart/graph and understand generally what's going on. It's worth the investment in time.
For the first question:
Note that it asks "which of the following MUST be true?" Simply try to imagine a scenario in which it isn't true and if you can, then it isn't correct.
A. Less than 55 percent were male managers.
We can answer this one without a calculator. 550 would be 55% of 1000, right? But the survey has 1200 people in it, so there must indeed be less than 55% male managers.
B. Of the male managers, more identified work experience as an important characteristic to consider than identified proficiency in English.
Trap! We see that more managers require work experience than English. If you assume now difference between the male and female managers' preferences, than this is true. But we shouldn't assume anything. What if male managers are less likely to identify work experience as important than female managers? Then this statement may not be true. So B is out.
C. Less than 60 percent of the male managers identified specific occupational skill as important to consider.
Basically the same trap as B. This one is also out.
For the second question:
If you look up the appropriate info you get 72% and 55%, respectively. Use the "change over original" formula. In this case the change is the difference between 72 and 55, or 17. The original would be 55. Thus, 17/55. Again, we don't need the slow, clunky calculator. These numbers look sloppy but if you multiply 17 by 3 you would get 51. Thus, 17/51 = 1/3 so 17/55 should be a little less than that. D fits.
For the third question:
This is an overlapping set. You can ID it because they can value following directions AND/OR computer expertise, or neither. The easiest way to do an overlapping set problem is NOT a Venn diagram, but an overlapping set matrix. It's not easy to depict in a comment box, though. Anyway, draw three vertical lines and three horizontal lines to make a table. In this problem, I'd label the columns "Follows Directions," or FD, and "Not Follows Directions," or NFD, and Total. The rows, similarly, will be labeled "Computer Expertise," or CE, "Not Computer Expertise," or NCE, and Total again. I've made a poor attempt at a matrix below. The upper left box represents the 48 percent who answered that they valued both qualities. We can look up from the table how many value CE and FD and fill those out as below. The total, 100, (since we're dealing in percents,) goes in the lower right.
|FD|NFD|Total
CE|48|---| 58
NCE|--|---|---
Total|65|---|100
Looks good. Now we can reason that every two columns should add up to the total column, and every two rows should add up to the third row. For example, if 58% value CE then 42% must NOT value it, since the two possibilities must add up to 100. If we fill out the rest of the table we should get something like this:
|FD|NFD|Total
CE|48| 10| 58
NCE|17| 25| 42
Total|65| 35|100
So 25% valued neither quality. It's D.
For the first question:
Note that it asks "which of the following MUST be true?" Simply try to imagine a scenario in which it isn't true and if you can, then it isn't correct.
A. Less than 55 percent were male managers.
We can answer this one without a calculator. 550 would be 55% of 1000, right? But the survey has 1200 people in it, so there must indeed be less than 55% male managers.
B. Of the male managers, more identified work experience as an important characteristic to consider than identified proficiency in English.
Trap! We see that more managers require work experience than English. If you assume now difference between the male and female managers' preferences, than this is true. But we shouldn't assume anything. What if male managers are less likely to identify work experience as important than female managers? Then this statement may not be true. So B is out.
C. Less than 60 percent of the male managers identified specific occupational skill as important to consider.
Basically the same trap as B. This one is also out.
For the second question:
If you look up the appropriate info you get 72% and 55%, respectively. Use the "change over original" formula. In this case the change is the difference between 72 and 55, or 17. The original would be 55. Thus, 17/55. Again, we don't need the slow, clunky calculator. These numbers look sloppy but if you multiply 17 by 3 you would get 51. Thus, 17/51 = 1/3 so 17/55 should be a little less than that. D fits.
For the third question:
This is an overlapping set. You can ID it because they can value following directions AND/OR computer expertise, or neither. The easiest way to do an overlapping set problem is NOT a Venn diagram, but an overlapping set matrix. It's not easy to depict in a comment box, though. Anyway, draw three vertical lines and three horizontal lines to make a table. In this problem, I'd label the columns "Follows Directions," or FD, and "Not Follows Directions," or NFD, and Total. The rows, similarly, will be labeled "Computer Expertise," or CE, "Not Computer Expertise," or NCE, and Total again. I've made a poor attempt at a matrix below. The upper left box represents the 48 percent who answered that they valued both qualities. We can look up from the table how many value CE and FD and fill those out as below. The total, 100, (since we're dealing in percents,) goes in the lower right.
|FD|NFD|Total
CE|48|---| 58
NCE|--|---|---
Total|65|---|100
Looks good. Now we can reason that every two columns should add up to the total column, and every two rows should add up to the third row. For example, if 58% value CE then 42% must NOT value it, since the two possibilities must add up to 100. If we fill out the rest of the table we should get something like this:
|FD|NFD|Total
CE|48| 10| 58
NCE|17| 25| 42
Total|65| 35|100
So 25% valued neither quality. It's D.
Re: A survey of 550 male managers and 650 female managers was c
[#permalink]
 03 Feb 2018, 03:58
03 Feb 2018, 03:58
Thank you.



