
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Exam grades among the students in Ms. Harshman’s class are n
[#permalink]
 28 Jul 2018, 16:34
28 Jul 2018, 16:34
3
Expert Reply
13
Bookmarks
Question Stats:
 55% (01:02) correct
55% (01:02) correct
 44% (01:05) wrong
44% (01:05) wrong  based on 165 sessions
based on 165 sessions
Hide Show timer Statistics
Exam grades among the students in Ms. Harshman’s class are normally distributed, and the 50th percentile is equal to a score of 77.
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Quantity A |
Quantity B |
The number of students who scored less than 80 on the exam |
The number of students who scored greater than 74 on the exam |
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Re: Exam grades among the students in Ms. Harshman’s class are n
[#permalink]
 13 Aug 2018, 04:33
13 Aug 2018, 04:33
3
Expert Reply
3
Bookmarks
Explanation
The normal distribution is symmetrical around the mean. For any symmetrical distribution, the mean equals the median (also known as the 50th percentile). Thus, the number of students who scored less than 3 points above the mean (77 + 3 = 80) must be the same as the number of students who scored greater than 3 points below the mean (77 – 3 = 74). As long as the boundary scores (80 and 74) are placed symmetrically around the mean, the distribution will have equal proportions. Draw the normal distribution plot if it is at all confusing:
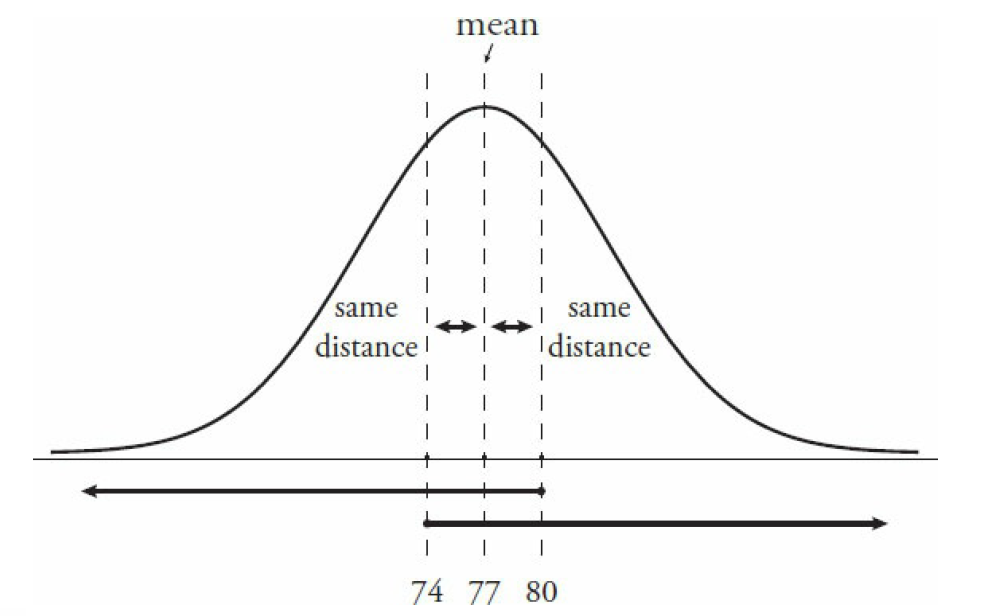
Capture.PNG [ 133.3 KiB | Viewed 12074 times ]
Notice that the two conditions overlap and are perfectly symmetrical. Each number consists of a short segment between it and the 50th percentile mark, as well as half of the students (either above or below the 50th percentile mark).
That is, the “less than 80” category consists of the segment between 80 and 77, as well as all students below the 50th percentile mark (below 77). The “greater than 74” category consists of the segment between 74 and 77, as well as all students above the 50th percentile mark (above 77). Therefore, the quantities are equal.
The normal distribution is symmetrical around the mean. For any symmetrical distribution, the mean equals the median (also known as the 50th percentile). Thus, the number of students who scored less than 3 points above the mean (77 + 3 = 80) must be the same as the number of students who scored greater than 3 points below the mean (77 – 3 = 74). As long as the boundary scores (80 and 74) are placed symmetrically around the mean, the distribution will have equal proportions. Draw the normal distribution plot if it is at all confusing:
Attachment:
Capture.PNG [ 133.3 KiB | Viewed 12074 times ]
Notice that the two conditions overlap and are perfectly symmetrical. Each number consists of a short segment between it and the 50th percentile mark, as well as half of the students (either above or below the 50th percentile mark).
That is, the “less than 80” category consists of the segment between 80 and 77, as well as all students below the 50th percentile mark (below 77). The “greater than 74” category consists of the segment between 74 and 77, as well as all students above the 50th percentile mark (above 77). Therefore, the quantities are equal.
General Discussion
Re: Exam grades among the students in Ms. Harshman’s class are n
[#permalink]
 09 Aug 2018, 06:53
09 Aug 2018, 06:53
2
Lets treat 50 percentile as 50% (number of )students scored 77 which means that the average mean or median is 77.
Now As normal distribution is mentioned if we go 3 S.D up on right side we get 80 and if we go 3 S.D. down which is left we get 74. So the number of students are going to be same.
As Each Standard Deviation will have X number of students and 3 S.d which up or down will be 3X hence same number of students.
Answer is C
Now As normal distribution is mentioned if we go 3 S.D up on right side we get 80 and if we go 3 S.D. down which is left we get 74. So the number of students are going to be same.
As Each Standard Deviation will have X number of students and 3 S.d which up or down will be 3X hence same number of students.
Answer is C






