GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Figure shown above consists of two squares having the same centers.
[#permalink]
09 Jan 2025, 01:45
09 Jan 2025, 01:45
Expert Reply
00:00
Question Stats:
100% (03:07) correct
0% (00:00) wrong based on 4 sessions
Hide Show timer Statistics
Attachment:
GRE shaded region square.png [ 16.61 KiB | Viewed 310 times ]
Figure shown above consists of two squares having the same centers. Sides of the inner square, each of length 4 units, are parallel to the sides of the outer square each having length of 12 units.
Quantity A |
Quantity B |
Perimeter of the shaded region |
Area of the shaded region |
- Part of the project: GRE Quant & Verbal ADVANCED Daily Challenge 2024 Edition - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
- Also replying to the unanswered questions
Re: Figure shown above consists of two squares having the same centers.
[#permalink]
18 Feb 2025, 04:05
18 Feb 2025, 04:05
Expert Reply
OFFICIAL EXPLANATION
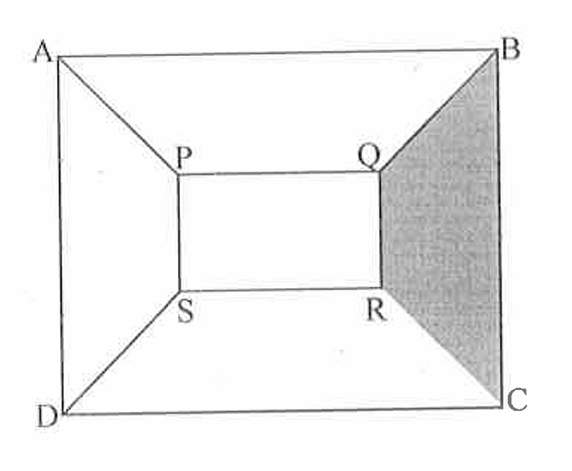
gre SQUARE.png [ 85.43 KiB | Viewed 21 times ]
The square ABCD having sides 12 unit's each, has diagonal $\(\mathrm{AC}(=\mathrm{BD})\)$ of length $\(12 \sqrt{2}\)$ (Diagonal in a square is $\(\sqrt{2}\)$ times the side).
Same way the diagonal of square PQRS having side 4 unit's each is $\(4 \sqrt{2}(=P R=Q S)\)$
Now, $\(A C-P R=12 \sqrt{2}-4 \sqrt{2}=8 \sqrt{2}\)$ is same as $\(A P+R C=2 R C\)$ (the figure has $\(A P=R C\)$ ), so we get $\(2 R C=8 \sqrt{2} \Rightarrow R C=4 \sqrt{2}\)$
Next the length of the sides of isosceles trapezium QRCB ; is $\(\mathrm{QR}=4, \mathrm{BC}=12 \& \mathrm{RC}=\mathrm{QB}=4 \sqrt{2}\)$
Finally the perimeter of the shaded region i.e. trapezium $\(Q R C B\)$ is $\(Q R+B C+R C+Q B=\)$ $\(4+12+4 \sqrt{2}+4 \sqrt{2}=16+8 \sqrt{2}(=$ Column A quantity $) \&\)$ the area of the shaded portion is $\(\frac{1}{2} \times\)($ Sum of parallel sides $) \(\times\)$ Distance between parallel sides $\(=\frac{1}{2} \times(4+12) \times 4=32(=\)$ column $\(B\)$ quantity)
Clearly $\(16+8 \sqrt{2}<32\)$ i.e. column $B$ has higher quantity when compared with column $\(A\)$.
Hence the answer is (B).
Attachment:
gre SQUARE.png [ 85.43 KiB | Viewed 21 times ]
The square ABCD having sides 12 unit's each, has diagonal $\(\mathrm{AC}(=\mathrm{BD})\)$ of length $\(12 \sqrt{2}\)$ (Diagonal in a square is $\(\sqrt{2}\)$ times the side).
Same way the diagonal of square PQRS having side 4 unit's each is $\(4 \sqrt{2}(=P R=Q S)\)$
Now, $\(A C-P R=12 \sqrt{2}-4 \sqrt{2}=8 \sqrt{2}\)$ is same as $\(A P+R C=2 R C\)$ (the figure has $\(A P=R C\)$ ), so we get $\(2 R C=8 \sqrt{2} \Rightarrow R C=4 \sqrt{2}\)$
Next the length of the sides of isosceles trapezium QRCB ; is $\(\mathrm{QR}=4, \mathrm{BC}=12 \& \mathrm{RC}=\mathrm{QB}=4 \sqrt{2}\)$
Finally the perimeter of the shaded region i.e. trapezium $\(Q R C B\)$ is $\(Q R+B C+R C+Q B=\)$ $\(4+12+4 \sqrt{2}+4 \sqrt{2}=16+8 \sqrt{2}(=$ Column A quantity $) \&\)$ the area of the shaded portion is $\(\frac{1}{2} \times\)($ Sum of parallel sides $) \(\times\)$ Distance between parallel sides $\(=\frac{1}{2} \times(4+12) \times 4=32(=\)$ column $\(B\)$ quantity)
Clearly $\(16+8 \sqrt{2}<32\)$ i.e. column $B$ has higher quantity when compared with column $\(A\)$.
Hence the answer is (B).
Re: Figure shown above consists of two squares having the same centers.
[#permalink]
18 Feb 2025, 04:08
18 Feb 2025, 04:08
Expert Reply
OFFICIAL EXPLANATION
As $\(\mathrm{AB}=\mathrm{AD}=10 \& \mathrm{BC}=\mathrm{CD}=5\)$, so the opposite angles must also be equal.
Let us assume the equal opposite angles as $\(x\)$ and $\(y\)$, we get the figure as
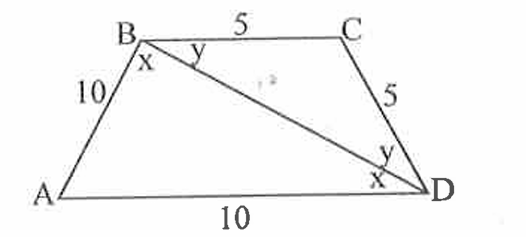
GRE PARALLELOGRAM.png [ 44.71 KiB | Viewed 17 times ]
If angle BAD is 60 degrees, the triangle ABD becomes equilateral and side BD comes 10 , which in triangle $\(B C D\)$ gives $\(B C+C D=5+5=10=B D\)$, which is not possible as the sum of the sides in a triangle is always greater than the third side.
To satisfy $\(\mathrm{BC}+\mathrm{CD}>\mathrm{BD}\)$, the length of BD must be less than 10 which implies the measure of angle opposite to side BD in triangle ABD must be less than 60 .
Hence only option (A) i.e. 45 degrees can be the measure of angle BAD, so is correct.
As $\(\mathrm{AB}=\mathrm{AD}=10 \& \mathrm{BC}=\mathrm{CD}=5\)$, so the opposite angles must also be equal.
Let us assume the equal opposite angles as $\(x\)$ and $\(y\)$, we get the figure as
Attachment:
GRE PARALLELOGRAM.png [ 44.71 KiB | Viewed 17 times ]
If angle BAD is 60 degrees, the triangle ABD becomes equilateral and side BD comes 10 , which in triangle $\(B C D\)$ gives $\(B C+C D=5+5=10=B D\)$, which is not possible as the sum of the sides in a triangle is always greater than the third side.
To satisfy $\(\mathrm{BC}+\mathrm{CD}>\mathrm{BD}\)$, the length of BD must be less than 10 which implies the measure of angle opposite to side BD in triangle ABD must be less than 60 .
Hence only option (A) i.e. 45 degrees can be the measure of angle BAD, so is correct.
