GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Give the right triangle ABC, find th slope of the segment
[#permalink]
11 Mar 2024, 06:19
11 Mar 2024, 06:19
Expert Reply
2
Bookmarks
00:00
Question Stats:
75% (03:38) correct
25% (02:37) wrong based on 4 sessions
Hide Show timer Statistics
Give the right triangle ABC, find the slope of the segment \(\overline{AB}\) and \(\overline{BC}\)
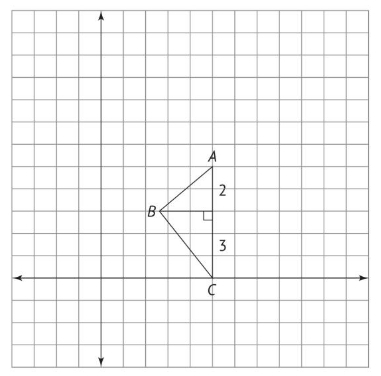
GRE xy.jpg [ 50.1 KiB | Viewed 545 times ]
A. \(\frac{2}{3}\) and \(- \frac{3}{2}\)
B. \(\dfrac{2}{\sqrt{6}}\) and \(\dfrac{-3}{\sqrt{6}}\)
C. \(\dfrac{2}{\sqrt{5}}\) and \(\dfrac{-\sqrt{5}}{2}\)
D. \(\dfrac{-3}{\sqrt{7}}\) and \(\dfrac{\sqrt{7}}{3}\)
E. cannot be determined
Attachment:
GRE xy.jpg [ 50.1 KiB | Viewed 545 times ]
A. \(\frac{2}{3}\) and \(- \frac{3}{2}\)
B. \(\dfrac{2}{\sqrt{6}}\) and \(\dfrac{-3}{\sqrt{6}}\)
C. \(\dfrac{2}{\sqrt{5}}\) and \(\dfrac{-\sqrt{5}}{2}\)
D. \(\dfrac{-3}{\sqrt{7}}\) and \(\dfrac{\sqrt{7}}{3}\)
E. cannot be determined
Part of the project: The Butler-GRE Daily New Quant and Verbal Questions to Practice (2023) - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
Re: Give the right triangle ABC, find th slope of the segment
[#permalink]
09 Apr 2024, 08:57
09 Apr 2024, 08:57
Expert Reply
OE
B. This problem tests your understanding of the proportions on a right triangle. Because of the orientation of the triangle, you can determine the rise for each segment. The missing part of the slope is the run, which corresponds to the height of the triangle (the unlabeled segment that intersects the hypotenuse at a right angle). Fortunately, this value can be found using the ratios of the proportions of a right triangle. Let the height of the triangle be h.
Use the ratios of the hypotenuses to find h:
short leg of the small triangle/hypotenuse of the small triangle=short leg of the large triangle/hypotenuse of the large triangle
\(\frac{2}{AB}=\frac{AB}{5}\)
\(10=AB^2\)
\(2^2+h^2=AB^2\)
\(h=\sqrt{6}\)
Now
slope \(\overline{AB}=\dfrac{2}{\sqrt{6}}=\dfrac{\sqrt{6}}{3}\)
slope \(\overline{BC}=\dfrac{-3}{\sqrt{6}}=\dfrac{- \sqrt{6}}{2}\)
B. This problem tests your understanding of the proportions on a right triangle. Because of the orientation of the triangle, you can determine the rise for each segment. The missing part of the slope is the run, which corresponds to the height of the triangle (the unlabeled segment that intersects the hypotenuse at a right angle). Fortunately, this value can be found using the ratios of the proportions of a right triangle. Let the height of the triangle be h.
Use the ratios of the hypotenuses to find h:
short leg of the small triangle/hypotenuse of the small triangle=short leg of the large triangle/hypotenuse of the large triangle
\(\frac{2}{AB}=\frac{AB}{5}\)
\(10=AB^2\)
\(2^2+h^2=AB^2\)
\(h=\sqrt{6}\)
Now
slope \(\overline{AB}=\dfrac{2}{\sqrt{6}}=\dfrac{\sqrt{6}}{3}\)
slope \(\overline{BC}=\dfrac{-3}{\sqrt{6}}=\dfrac{- \sqrt{6}}{2}\)
gmatclubot
Re: Give the right triangle ABC, find th slope of the segment [#permalink]
09 Apr 2024, 08:57
Moderators:
