
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
GRE Geometry Formulas for a Q170
[#permalink]
 27 Oct 2021, 12:48
27 Oct 2021, 12:48
2
Expert Reply

GRE Geometry Formulas for a Q170 Score
Show: ::
Attachment:
GRE Geometry Formullas Symbols.jpg [ 238.44 KiB | Viewed 2178 times ]
Attachment:
GRE geometry Formulas Circle and Triangle.jpg [ 281.72 KiB | Viewed 2389 times ]
Attachment:
GRE Geometry Formulas 3d shapes.jpg [ 189.71 KiB | Viewed 2405 times ]
Attachment:
GRE geometry Formulas Solid.jpg [ 135.74 KiB | Viewed 2231 times ]
GRE Geometry Formulas for a Q170
[#permalink]
 27 Oct 2021, 13:29
27 Oct 2021, 13:29
Expert Reply
Notation for Geometry:
A = area, P = perimeter, C = circumference
V = volume, H = Height, hyp = Hypotenuse
ANGLES and PARALLELS
(a) Two straight lines which meet at a point form an angle between them.
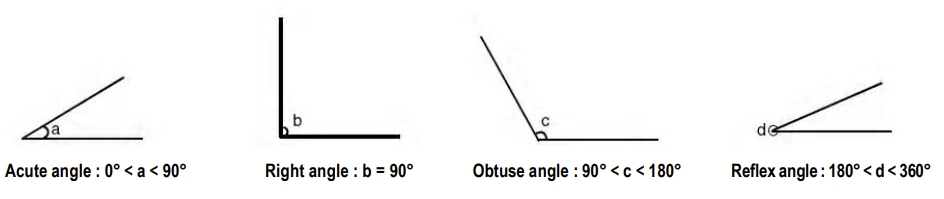
(b) Theorems :
1. If AOB is a straight line, then

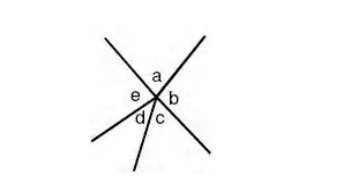
2. The sum of all the angle at a point, each being adjacent to the next, is 4 right angles.
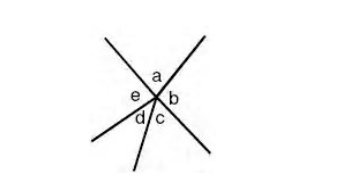
⇒ a + b + c + d + e = 360° (Angles at a point)
3. If two straight lines intersect, the vertically opposite angles are equal.
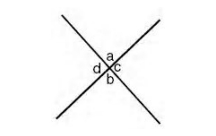
a = b, c = d (Vertically Opposite angles)
4. Parallel lines PQ and RS are cut by a transversal LM, then we have :
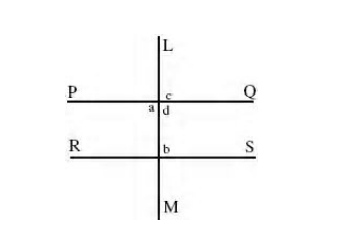
The corresponding angles are equal c = b (Corresponding angles, PQ || RS)
The alternate angles are equal a = b (Alternate angles, PQ || RS)
The interior angles are supplementary b + d = 2 right angles (Interior angles, PQ || RS)
5. (i) Two angles whose sum is 90°, are complementary. Each one is the complement of the other.
(ii) Two angles whose sum is 180º, are supplementary. Each one is the supplement of the other.
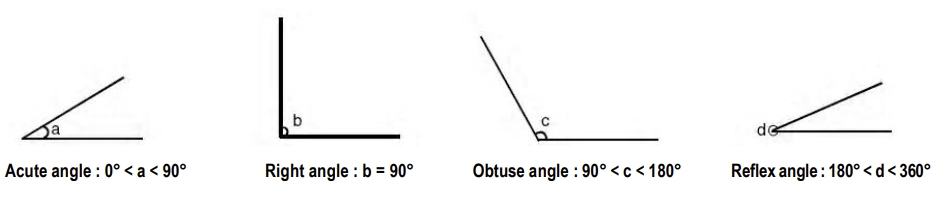
GRE angles.jpg [ 48.08 KiB | Viewed 2231 times ]

GRe 180.jpg [ 26.33 KiB | Viewed 2006 times ]
GRE angle.jpg [ 10.7 KiB | Viewed 1998 times ]
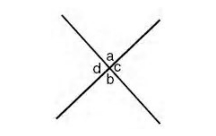
GRE opposite angle.jpg [ 7.46 KiB | Viewed 1995 times ]
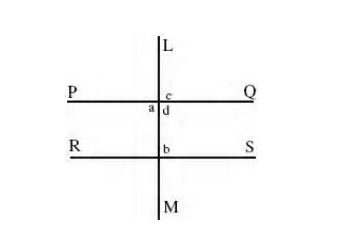
GRe parallel.jpg [ 10.38 KiB | Viewed 1988 times ]
A = area, P = perimeter, C = circumference
V = volume, H = Height, hyp = Hypotenuse
ANGLES and PARALLELS
(a) Two straight lines which meet at a point form an angle between them.
(b) Theorems :
1. If AOB is a straight line, then
2. The sum of all the angle at a point, each being adjacent to the next, is 4 right angles.
⇒ a + b + c + d + e = 360° (Angles at a point)
3. If two straight lines intersect, the vertically opposite angles are equal.
a = b, c = d (Vertically Opposite angles)
4. Parallel lines PQ and RS are cut by a transversal LM, then we have :
The corresponding angles are equal c = b (Corresponding angles, PQ || RS)
The alternate angles are equal a = b (Alternate angles, PQ || RS)
The interior angles are supplementary b + d = 2 right angles (Interior angles, PQ || RS)
5. (i) Two angles whose sum is 90°, are complementary. Each one is the complement of the other.
(ii) Two angles whose sum is 180º, are supplementary. Each one is the supplement of the other.
Show: ::
Attachment:
GRE angles.jpg [ 48.08 KiB | Viewed 2231 times ]
Attachment:
GRe 180.jpg [ 26.33 KiB | Viewed 2006 times ]
Attachment:
GRE angle.jpg [ 10.7 KiB | Viewed 1998 times ]
Attachment:
GRE opposite angle.jpg [ 7.46 KiB | Viewed 1995 times ]
Attachment:
GRe parallel.jpg [ 10.38 KiB | Viewed 1988 times ]
GRE Geometry Formulas for a Q170
[#permalink]
 28 Oct 2021, 11:42
28 Oct 2021, 11:42
Expert Reply
A closed figure enclosed by 3 sides is called a Triangle. ABC is a triangle. The sides AB, BC, AC are respectively denoted by c, a, b. Please carefully note the capital and small letters.
In any triangle ABC
(1) \(A = \frac{1}{2} a \times h = \frac{1}{2} base\) \(\times\) perpendicular to base from opposite vertex
(2) \(A = \sqrt{s(s –a)(s – b)(s – c)}\) , \(s = \frac{(a + b + c)}{2} =\) semi–perimeter
(3) \(P = (a + b + c) = 2 s\)
PROPERTIES :
1. Sum of the three interior angles is 180°
2. When one side is extended in any direction, an angle is formed with another side. This is called the exterior angle.
3. There are six exterior angles of a triangle.
4. Interior angle + corresponding exterior angle = 180°.
5. An exterior angle = Sum of the other two interior angles not adjacent to it
6. Sum of any two sides is greater than the third side.
7. Difference of any two sides is less than the third side.
8. Side opposite to the greatest angle will be the greatest and vice versa.
9. A triangle must have at least two acute angles.
10. Triangles on equal bases and between the same parallels have equal areas.
11. If a, b, c denote the sides of a triangle then
(i) if \(c^2 < a^2 + b^2\), Triangle is acute angled
(ii) if \(c^2 = a^2 + b^2\), Triangle is right angled
(iii) if \(c^2 > a^2 + b^2\), Triangle is obtuse angled
Right Angled Triangle
A triangle whose one angle is 90° is called a right (angled) Triangle. In the figure, b is the hypotenuse, and a & c the legs, called base and height resp.
(1) \(h^2 = m n\)
(2) \(AC^2 = AB^2 + BC^2\) (Pythagoras theorem)
(3) \(h = \frac{ac}{b}\)
(4) \(Area = \frac{ac }{ 2}\)
NOTE : You should remember some of the Pythagorean triplets (e.g. 3,4,5 because \(5² = 3² + 4²\)). Some others are (5, 12, 13), (7, 24, 25) etc.
Show: ::
Attachment:
GRE triangles.jpg [ 20.33 KiB | Viewed 1931 times ]
Attachment:
GRE right angled.jpg [ 13.93 KiB | Viewed 1919 times ]
Attachment:
GRE triplets.jpg [ 139.99 KiB | Viewed 1918 times ]

