Circle on a plane

In an x-y Cartesian coordinate system, the circle with center (a, b) and radius r is the set of all points (x, y) such that:
\((x-a)^2+(y-b)^2=r^2\)




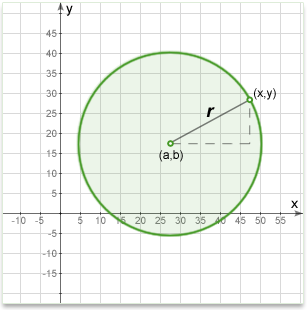
This equation of the circle follows from the Pythagorean theorem applied to any point on the circle: as shown in the diagram above, the radius is the hypotenuse of a right-angled triangle whose other sides are of length x-a and y-b.

If the circle is centered at the origin (0, 0), then the equation simplifies to:
\(x^2+y^2=r^2\)


Number line

A number line is a picture of a straight line on which every point corresponds to a real number and every real number to a point.




On the GMAT we can often see such statement: \(k\) is halfway between \(m\) and \(n\) on the number line. Remember this statement can ALWAYS be expressed as:

\(\frac{m+n}{2}=k\).

Also on the GRE we can often see another statement: The distance between \(p\) and \(m\) on the number line is the same as the distance between \(p\) and \(n\). Remember this statement can ALWAYS be expressed as:
\(|p-m|=|p-n|\)