
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
GRE Quant - Coordinate Geometry Parabolas Theory
[#permalink]
 25 Jun 2020, 13:51
25 Jun 2020, 13:51
4
1
Expert Reply
5
Bookmarks
Frequency of the concepts tested: Low
Parabola
A parabola is the graph associated with a quadratic function, i.e. a function of the form \(y=ax^2+bx+c\).
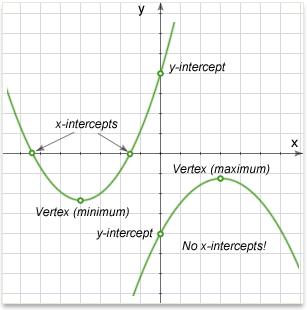
The general or standard form of a quadratic function is \(y =ax^2+bx+c\), or in function form, \(f(x)=ax^2+bx+c\), where \(x\) is the independent variable, \(y\) is the dependent variable, and \(a\), \(b\), and \(c\) are constants.
x-intercepts: The x-intercepts, if any, are also called the roots of the function. The x-intercepts are the solutions to the equation \(0=ax^2+bx+c\) and can be calculated by the formula:
\(x_1=\frac{-b-\sqrt{b^2-4ac}}{2a}\) and \(x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}\)
Expression \(b^2-4ac\) is called discriminant:
y-intercept: Given \(y =ax^2+bx+c\), the y-intercept is \(c\), as y intercept means the value of y when x=0.
Vertex: The vertex represents the maximum (or minimum) value of the function, and is very important in calculus.
The vertex of the parabola is located at point \((-\frac{b}{2a},\) \(c-\frac{b^2}{4a})\).
Note: typically just \(-\frac{b}{2a},\) is calculated and plugged in for x to find y.
A parabola is the graph associated with a quadratic function, i.e. a function of the form \(y=ax^2+bx+c\).
The general or standard form of a quadratic function is \(y =ax^2+bx+c\), or in function form, \(f(x)=ax^2+bx+c\), where \(x\) is the independent variable, \(y\) is the dependent variable, and \(a\), \(b\), and \(c\) are constants.
- The larger the absolute value of \(a\), the steeper (or thinner) the parabola is, since the value of y is increased more quickly.
- If \(a\) is positive, the parabola opens upward, if negative, the parabola opens downward.
x-intercepts: The x-intercepts, if any, are also called the roots of the function. The x-intercepts are the solutions to the equation \(0=ax^2+bx+c\) and can be calculated by the formula:
\(x_1=\frac{-b-\sqrt{b^2-4ac}}{2a}\) and \(x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}\)
Expression \(b^2-4ac\) is called discriminant:
- If discriminant is positive parabola has two intercepts with x-axis;
- If discriminant is negative parabola has no intercepts with x-axis;
- If discriminant is zero parabola has one intercept with x-axis (tangent point).
y-intercept: Given \(y =ax^2+bx+c\), the y-intercept is \(c\), as y intercept means the value of y when x=0.
Vertex: The vertex represents the maximum (or minimum) value of the function, and is very important in calculus.
The vertex of the parabola is located at point \((-\frac{b}{2a},\) \(c-\frac{b^2}{4a})\).
Note: typically just \(-\frac{b}{2a},\) is calculated and plugged in for x to find y.
Re: GRE Quant - Coordinate Geometry Parabolas Theory
[#permalink]
 11 Jul 2020, 11:19
11 Jul 2020, 11:19
Expert Reply
Coordinate Geometry Parabolas Questions by Tag
Quantitative Comparison Questions
Multiple-choice Questions — Select One Answer Choice
Multiple-choice Questions — Select One or More Answer Choices
Numeric Entry Question
Data Interpretation Sets
HARD QuestionsMEDIUM QuestionsEASY Questions


