
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
GRE Quant - Special Triangles Theory
[#permalink]
 Updated on: 25 Mar 2025, 07:25
Updated on: 25 Mar 2025, 07:25
3
Expert Reply
4
Bookmarks
Frequency of the concepts tested: Medium
Scalene triangle all sides and angles are different from one another
• All properties mentioned above can be applied to the scalene triangle, if not mentioned the special cases (equilateral, etc)
Equilateral triangle all sides have the same length.

• An equilateral triangle is also a regular polygon with all angles measuring 60°.
• The area is \(A=a^2*\frac{\sqrt{3}}{4}\)
• The perimeter is \(P=3a\)
• The radius of the circumscribed circle is \(R=a*\frac{\sqrt{3}}{3}\)
• The radius of the inscribed circle is \(r=a*\frac{\sqrt{3}}{6}\)
• And the altitude is \(h=a*\frac{\sqrt{3}}{2}\) (Where \(a\) is the length of a side.)
• For any point P within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle.
• For a given perimeter equilateral triangle has the largest area.
• For a given area equilateral triangle has the smallest perimeter.
• With an equilateral triangle, the radius of the incircle is exactly half the radius of the circumcircle.
Isosceles triangle two sides are equal in length.

• An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length.
• For an isosceles triangle with given length of equal sides right triangle (included angle) has the largest area.
• To find the base given the leg and altitude, use the formula: \(B=2\sqrt{L^2-A^2}\)
• To find the leg length given the base and altitude, use the formula: \(L=\sqrt{A^2+(\frac{B}{2})^2}\)
• To find the altitude given the base and leg, use the formula: \(A=\sqrt{L^2-(\frac{B}{2})^2}\) (Where: L is the length of a leg; A is the altitude; B is the length of the base)
Right triangle A triangle where one of its interior angles is a right angle (90 degrees)
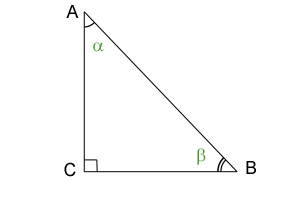
• Hypotenuse: the side opposite the right angle. This will always be the longest side of a right triangle.
• The two sides that are not the hypotenuse. They are the two sides making up the right angle itself.
• Theorem by Pythagoras defines the relationship between the three sides of a right triangle: \(a^2 + b^2 = c^2\), where \(c\) is the length of the hypotenuse and \(a\), \(b\) are the lengths of the the other two sides.
• In a right triangle, the midpoint of the hypotenuse is equidistant from the three polygon vertices
• A right triangle can also be isosceles if the two sides that include the right angle are equal in length (AC and BC in the figure above)
• Right triangle with a given hypotenuse has the largest area when it's an isosceles triangle.
• A right triangle can never be equilateral, since the hypotenuse (the side opposite the right angle) is always longer than the other two sides.
• Any triangle whose sides are in the ratio 3:4:5 is a right triangle. Such triangles that have their sides in the ratio of whole numbers are called Pythagorean Triples. There are an infinite number of them, and this is just the smallest. If you multiply the sides by any number, the result will still be a right triangle whose sides are in the ratio 3:4:5. For example 6, 8, and 10.
• A Pythagorean triple consists of three positive integers \(a\), \(b\), and \(c\), such that \(a^2 + b^2 = c^2\). Such a triple is commonly written \((a, b, c)\), and a well-known example is \((3, 4, 5)\). If \((a, b, c)\) is a Pythagorean triple, then so is \((ka, kb, kc)\) for any positive integer \(k\).
There are 16 primitive Pythagorean triples with \(c ≤ 100\):
(3, 4, 5) (5, 12, 13) (7, 24, 25) (8, 15, 17) (9, 40, 41) (11, 60, 61) (12, 35, 37) (13, 84, 85) (16, 63, 65) (20, 21, 29) (28, 45, 53) (33, 56, 65) (36, 77, 85) (39, 80, 89) (48, 55, 73) (65, 72, 97).
However, the GRE will suffice to memorize the following Pythagorean triples
• A right triangle where the angles are 30°, 60°, and 90°.

This is one of the 'standard' triangles you should be able recognize on sight. A fact you should commit to memory is: The sides are always in the ratio \(1 : \sqrt{3}: 2\).
Notice that the smallest side (1) is opposite the smallest angle (30°), and the longest side (2) is opposite the largest angle (90°).
• A right triangle where the angles are 45°, 45°, and 90°.

This is one of the 'standard' triangles you should be able recognize on sight. A fact you should also commit to memory is: The sides are always in the ratio \(1 : 1 : \sqrt{2}\). With the \(\sqrt{2}\) being the hypotenuse (longest side). This can be derived from Pythagoras' Theorem. Because the base angles are the same (both 45°) the two legs are equal and so the triangle is also isosceles.
• Area of a 45-45-90 triangle. As you see from the figure above, two 45-45-90 triangles together make a square, so the area of one of them is half the area of the square. As a formula \(A=\frac{S^2}{2}\). Where S is the length of either short side.
• Right triangle inscribed in circle:
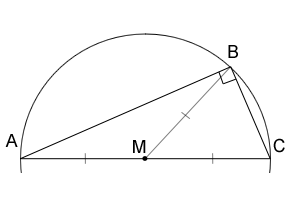
\(R = \frac{AC}{2}\)
• If M is the midpoint of the hypotenuse, then \(BM = \frac{1}{2}AC\). One can also say that point B is located on the circle with diameter \(AC\). Conversely, if B is any point of the circle with diameter \(AC\) (except A or C themselves) then angle B in triangle ABC is a right angle.
• A right triangle inscribed in a circle must have its hypotenuse as the diameter of the circle. The reverse is also true: if the diameter of the circle is also the triangle’s hypotenuse, then that triangle is a right triangle.
• Circle inscribed in right triangle: \(r = \frac{ab}{a+b+c}=\frac{a+b-c}{2}\)
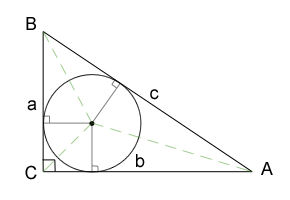
Note that in picture above the right angle is C.
• Given a right triangle, draw the altitude from the right angle.
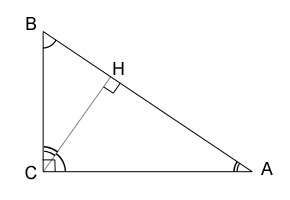
Then the triangles ABC, CHB and CHA are similar. Perpendicular to the hypotenuse will always divide the triangle into two triangles with the same properties as the original triangle.
• All properties mentioned above can be applied to the scalene triangle, if not mentioned the special cases (equilateral, etc)
Equilateral triangle all sides have the same length.
• An equilateral triangle is also a regular polygon with all angles measuring 60°.
• The area is \(A=a^2*\frac{\sqrt{3}}{4}\)
• The perimeter is \(P=3a\)
• The radius of the circumscribed circle is \(R=a*\frac{\sqrt{3}}{3}\)
• The radius of the inscribed circle is \(r=a*\frac{\sqrt{3}}{6}\)
• And the altitude is \(h=a*\frac{\sqrt{3}}{2}\) (Where \(a\) is the length of a side.)
• For any point P within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle.
• For a given perimeter equilateral triangle has the largest area.
• For a given area equilateral triangle has the smallest perimeter.
• With an equilateral triangle, the radius of the incircle is exactly half the radius of the circumcircle.
Isosceles triangle two sides are equal in length.
• An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length.
• For an isosceles triangle with given length of equal sides right triangle (included angle) has the largest area.
• To find the base given the leg and altitude, use the formula: \(B=2\sqrt{L^2-A^2}\)
• To find the leg length given the base and altitude, use the formula: \(L=\sqrt{A^2+(\frac{B}{2})^2}\)
• To find the altitude given the base and leg, use the formula: \(A=\sqrt{L^2-(\frac{B}{2})^2}\) (Where: L is the length of a leg; A is the altitude; B is the length of the base)
Right triangle A triangle where one of its interior angles is a right angle (90 degrees)
• Hypotenuse: the side opposite the right angle. This will always be the longest side of a right triangle.
• The two sides that are not the hypotenuse. They are the two sides making up the right angle itself.
• Theorem by Pythagoras defines the relationship between the three sides of a right triangle: \(a^2 + b^2 = c^2\), where \(c\) is the length of the hypotenuse and \(a\), \(b\) are the lengths of the the other two sides.
• In a right triangle, the midpoint of the hypotenuse is equidistant from the three polygon vertices
• A right triangle can also be isosceles if the two sides that include the right angle are equal in length (AC and BC in the figure above)
• Right triangle with a given hypotenuse has the largest area when it's an isosceles triangle.
• A right triangle can never be equilateral, since the hypotenuse (the side opposite the right angle) is always longer than the other two sides.
• Any triangle whose sides are in the ratio 3:4:5 is a right triangle. Such triangles that have their sides in the ratio of whole numbers are called Pythagorean Triples. There are an infinite number of them, and this is just the smallest. If you multiply the sides by any number, the result will still be a right triangle whose sides are in the ratio 3:4:5. For example 6, 8, and 10.
• A Pythagorean triple consists of three positive integers \(a\), \(b\), and \(c\), such that \(a^2 + b^2 = c^2\). Such a triple is commonly written \((a, b, c)\), and a well-known example is \((3, 4, 5)\). If \((a, b, c)\) is a Pythagorean triple, then so is \((ka, kb, kc)\) for any positive integer \(k\).
There are 16 primitive Pythagorean triples with \(c ≤ 100\):
(3, 4, 5) (5, 12, 13) (7, 24, 25) (8, 15, 17) (9, 40, 41) (11, 60, 61) (12, 35, 37) (13, 84, 85) (16, 63, 65) (20, 21, 29) (28, 45, 53) (33, 56, 65) (36, 77, 85) (39, 80, 89) (48, 55, 73) (65, 72, 97).
However, the GRE will suffice to memorize the following Pythagorean triples
| TRIPLE | Multiples |
| 3:4:5 | 6:8:10 |
| 5:12:13 | 10:24:26 |
| 7:24:25 | 14:48:50 |
| 8:15:17 | 16:30:34 |
| 9:40:41 | |
| 12:35:37 | |
| 20:21:29 |
• A right triangle where the angles are 30°, 60°, and 90°.
This is one of the 'standard' triangles you should be able recognize on sight. A fact you should commit to memory is: The sides are always in the ratio \(1 : \sqrt{3}: 2\).
Notice that the smallest side (1) is opposite the smallest angle (30°), and the longest side (2) is opposite the largest angle (90°).
• A right triangle where the angles are 45°, 45°, and 90°.
This is one of the 'standard' triangles you should be able recognize on sight. A fact you should also commit to memory is: The sides are always in the ratio \(1 : 1 : \sqrt{2}\). With the \(\sqrt{2}\) being the hypotenuse (longest side). This can be derived from Pythagoras' Theorem. Because the base angles are the same (both 45°) the two legs are equal and so the triangle is also isosceles.
• Area of a 45-45-90 triangle. As you see from the figure above, two 45-45-90 triangles together make a square, so the area of one of them is half the area of the square. As a formula \(A=\frac{S^2}{2}\). Where S is the length of either short side.
• Right triangle inscribed in circle:
\(R = \frac{AC}{2}\)
• If M is the midpoint of the hypotenuse, then \(BM = \frac{1}{2}AC\). One can also say that point B is located on the circle with diameter \(AC\). Conversely, if B is any point of the circle with diameter \(AC\) (except A or C themselves) then angle B in triangle ABC is a right angle.
• A right triangle inscribed in a circle must have its hypotenuse as the diameter of the circle. The reverse is also true: if the diameter of the circle is also the triangle’s hypotenuse, then that triangle is a right triangle.
• Circle inscribed in right triangle: \(r = \frac{ab}{a+b+c}=\frac{a+b-c}{2}\)
Note that in picture above the right angle is C.
• Given a right triangle, draw the altitude from the right angle.
Then the triangles ABC, CHB and CHA are similar. Perpendicular to the hypotenuse will always divide the triangle into two triangles with the same properties as the original triangle.
Re: GRE Quant - Special Triangles Theory
[#permalink]
 11 Jul 2020, 10:43
11 Jul 2020, 10:43
Expert Reply
1
Bookmarks
Special Triangles Questions by Tag
Quantitative Comparison Questions
Multiple-choice Questions — Select One Answer Choice
Multiple-choice Questions — Select One or More Answer Choices
Numeric Entry Question
Data Interpretation Sets
HARD QuestionsMEDIUM QuestionsEASY Questions


