
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
In a survey, 86 high school students were randomly selected
[#permalink]
 15 Oct 2017, 22:42
15 Oct 2017, 22:42
2
8
Bookmarks
Question Stats:
 55% (01:58) correct
55% (01:58) correct
 44% (01:51) wrong
44% (01:51) wrong  based on 76 sessions
based on 76 sessions
Hide Show timer Statistics
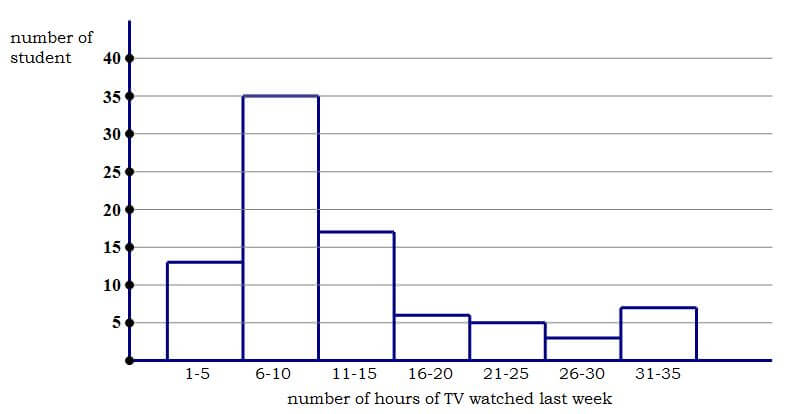
In a survey, 86 high school students were randomly selected and asked how many hours of television they had watched in the previous week. The histogram below displays their answers.
A. The quantity in Column A is greater
B. The quantity in Column B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Kudos for correct solution.

newest-histogram.jpg [ 21.04 KiB | Viewed 17255 times ]
Quantity A |
Quantity B |
The mean number of hours of TV watched last week |
The median number of hours of TV watched last week |
A. The quantity in Column A is greater
B. The quantity in Column B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Kudos for correct solution.
Show: ::
Attachment:
newest-histogram.jpg [ 21.04 KiB | Viewed 17255 times ]
Re: In a survey, 86 high school students were randomly selected
[#permalink]
 15 Oct 2017, 23:54
15 Oct 2017, 23:54
2
An easy trick to solve it is to notice that this distribution has a long right hand tail, meaning that there are individuals with high values of hours spent on TV (higher mean) but they are few (the median is low). Thus, the mean is higher than the median and answer is A
Re: In a survey, 86 high school students were randomly selected
[#permalink]
 29 Nov 2017, 04:13
29 Nov 2017, 04:13
4
If I had gotten this one wrong, I probably would have given up my plans to become a statistician!!!!!!!
The median is basically the number in a set that is right in the middle of the set. In order to find the median, you first need to WRITE THE NUMBERS IN A SET IN ASCENDING ORDER.
3 - 5 - 6 - 7 - 13 - 17 - 35
Now we need to look at the set and decide which number is in the middle. 7 is the best choice because there are exacltly 3 numbers to its right (13, 17 and 35) and 3 numbers to its left (3.5 and 6).
Qunatity B is thus 7.
The mean is the avarage of all numbers in a set. All we need to do is add all numbers together and divide the result by how many numbeers there are in the set.
3 + 5 + 6 + 7 + 13 + 17 + 35 = 86
There are 7 numbers in this set.
86/7 = 12.3
Quantity A is 12.3
Qunaity A is greater than quantity B. A is the answer.
This histogram can be a bit tricky to read so I may have gotten some of the numbers wrong.
The median is basically the number in a set that is right in the middle of the set. In order to find the median, you first need to WRITE THE NUMBERS IN A SET IN ASCENDING ORDER.
3 - 5 - 6 - 7 - 13 - 17 - 35
Now we need to look at the set and decide which number is in the middle. 7 is the best choice because there are exacltly 3 numbers to its right (13, 17 and 35) and 3 numbers to its left (3.5 and 6).
Qunatity B is thus 7.
The mean is the avarage of all numbers in a set. All we need to do is add all numbers together and divide the result by how many numbeers there are in the set.
3 + 5 + 6 + 7 + 13 + 17 + 35 = 86
There are 7 numbers in this set.
86/7 = 12.3
Quantity A is 12.3
Qunaity A is greater than quantity B. A is the answer.
This histogram can be a bit tricky to read so I may have gotten some of the numbers wrong.









