GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
In the figure above, triangle ABC is equilateral, and point
[#permalink]
03 Apr 2020, 08:26
03 Apr 2020, 08:26
1
Expert Reply
00:00
Question Stats:
60% (01:02) correct
40% (00:34) wrong based on 5 sessions
Hide Show timer Statistics
In the figure above, triangle ABC is equilateral, and point P is equidistant from vertices A, B, and C. If triangle ABC is rotated clockwise about point P, what is the minimum number of degrees the triangle must be rotated so that point B will be in the position where point A is now?
(A) 60
(B) 120
(C) 180
(D) 240
(E) 270
Kudos for the right answer and explanation
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: In the figure above, triangle ABC is equilateral, and point
[#permalink]
03 Apr 2020, 08:36
03 Apr 2020, 08:36
Carcass wrote:
In the figure above, triangle ABC is equilateral, and point P is equidistant from vertices A, B, and C. If triangle ABC is rotated clockwise about point P, what is the minimum number of degrees the triangle must be rotated so that point B will be in the position where point A is now?
(A) 60
(B) 120
(C) 180
(D) 240
(E) 270
Kudos for the right answer and explanation
It may help to add some lines to the diagram.
First add lines from the center to the 3 vertices.
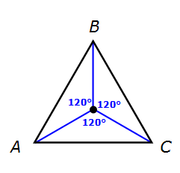
Aside, we know that each angle is 120º since all three (equivalent) angles must add to 360º
Then draw a circle so that the triangles vertices are on the circle.
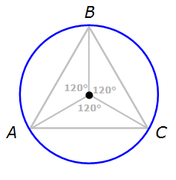
From here, we can see that . ..
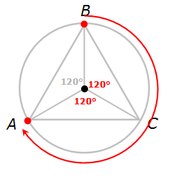
. . . the triangle must be rotated clockwise 240º in order for point B to be in the position where point A is now.
Answer: D
Cheers,
Brent
gmatclubot
Re: In the figure above, triangle ABC is equilateral, and point [#permalink]
03 Apr 2020, 08:36
Moderators:
