GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Apr 25Crafting an Impactful Resume: Balancing Detail with Brevity
10:00 AM EDT
-10:30 AM EDT
Showcase your achievements through impactful storytelling! Get ready for an LIVE session on April 25, Learn how to craft compelling narratives on your resume that resonate with admission committees.
Apr 24Get an Extra 30% Off Target Test Prep Plans
08:00 PM EDT
-11:59 PM EDT
Grab 30% off any Target Test Prep GRE plan during our Flash Sale and join Brian and many other students who have used Target Test Prep to score high on the GRE. Just enter the coupon code FLASH30 at checkout to save big.
Apr 26Get a Top GRE Score with Target Test Prep
12:00 PM EDT
-01:00 PM EDT
The Target Test Prep course represents a quantum leap forward in GRE preparation, a radical reinterpretation of the way that students should study. In fact, more and more Target Test Prep students are scoring 329 and above on the GRE.
In the figure below, If the area of triangle CDE is 42, what
[#permalink]
26 May 2019, 01:46
26 May 2019, 01:46
Expert Reply
10
Bookmarks
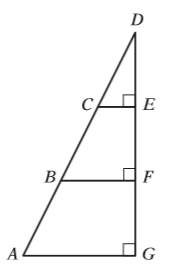
In the figure below, AB=BC=CD. If the area of triangle CDE is 42, what is the area of triangle ADG?
#GREexcercise In the figure below, If the area of triangle CDE is 42, what is AB=BC=CD..jpg [ 10.08 KiB | Viewed 52590 times ]
Attachment:
#GREexcercise In the figure below, If the area of triangle CDE is 42, what is AB=BC=CD..jpg [ 10.08 KiB | Viewed 52590 times ]
Show: :: OA
378
Math Review
Question: 9
Page: 260
Difficulty: medium
Question: 9
Page: 260
Difficulty: medium
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: In the figure below, If the area of triangle CDE is 42, what
[#permalink]
29 May 2019, 07:55
29 May 2019, 07:55
12
2
Bookmarks
Carcass wrote:
In the figure below, AB=BC=CD. If the area of triangle CDE is 42, what is the area of triangle ADG?
Attachment:
#GREexcercise In the figure below, If the area of triangle CDE is 42, what is AB=BC=CD..jpg
Show: :: OA
378
Math Review
Question: 9
Page: 260
Difficulty: medium
Question: 9
Page: 260
Difficulty: medium
Let's add the given information to the diagram.
Notice that the angles (represented by blue dots) are all equal.
If we draw some auxiliary lines from points B and C....
...we find that we have 3 IDENTICAL right triangles
If we let y = the base of ∆CDE and let x = the height of ∆CDE...
...then we can add several more x's and y's to the diagram.
From this, we can see that...
...the base of ∆ADG has length 3y and a height of 3x
GIVEN: the area of ∆CDE is 42
Area of triangle = (base)(height)/2
So, we can write: (y)(x)/2 = 42
This means: yx = 84
We're asked to find the area of ∆ADG
Area of triangle = (base)(height)/2
So, the area of ∆ADG = (3y)(3x)/2
= 9yx/2
Since we know that yx = 84, we can replace yx with 84 to get:
Area of ∆ADG = 9(84)/2 = 378
Answer: 378
Cheers,
Brent
General Discussion
Re: In the figure below, If the area of triangle CDE is 42, what
[#permalink]
26 May 2019, 19:20
26 May 2019, 19:20
6
Carcass wrote:
In the figure below,AB=BC=CD. If the area of triangle CDE is 42, what is the area of triangle ADG?
Attachment:
#GREexcercise In the figure below, If the area of triangle CDE is 42, what is AB=BC=CD..jpg
Show: :: OA
378
Math Review
Question: 9
Page: 260
Difficulty: medium
Question: 9
Page: 260
Difficulty: medium
Here,
all the three triangles ( \(\triangle\)CDE , \(\triangle\) BDF and \(\triangle\) ADG are similar)
and one side of the \(\triangle\) CDE = \(\frac{1}{3}\)of the \(\triangle\) ADG
Hence the Area of \(\triangle\)ADG = \((\frac{1}{2} * AG * DG) = (\frac{1}{2} * 3CE * 3DE) = 9 * (\frac{1}{2} * CE * DE)\) = 9 * Area of the \(\triangle\) CDE = \(9 * 42 = 378\)
