
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
In triangle ABC, the measure of angle B is 90°, the length o
[#permalink]
 Updated on: 12 Jul 2021, 05:43
Updated on: 12 Jul 2021, 05:43
3
1
Expert Reply
11
Bookmarks
Question Stats:
 47% (02:07) correct
47% (02:07) correct
 52% (01:56) wrong
52% (01:56) wrong  based on 140 sessions
based on 140 sessions
Hide Show timer Statistics
In triangle ABC, the measure of angle B is 90°, the length of side AB is 4, and the length of side BC is x. If the length of hypotenuse AC is between 4 and 8, which of the following could be the value of x ?
Indicate \(all\) such values.
❑ 1
❑ 2
❑ 3
❑ 4
❑ 5
❑ 6
Indicate \(all\) such values.
❑ 1
❑ 2
❑ 3
❑ 4
❑ 5
❑ 6
ShowHide Answer
Official Answer
A,B,C,D,E,F
Re: In triangle ABC, the measure of angle B is 90°, the length o
[#permalink]
 27 Nov 2017, 16:46
27 Nov 2017, 16:46
4
Expert Reply
1
Bookmarks
Look at the figure below:
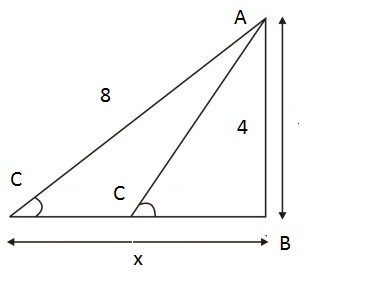
Length of side AB is 4, and the length of side BC is xand AC is between 4 and 8. There can be many triangles that satify this condition.
On one extreme when AC is almost 4. Then the the triangle becomes almost the line AB and \(x\) is almost 0.
On the other hand when AC is 8 then \(x=\sqrt{8^2-4^2} \approx 6.9\).
So all values from 0 to 6.9 form a right triangle. Hence all options are correct!
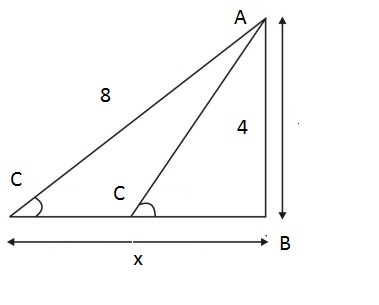
right.jpg [ 13.28 KiB | Viewed 39407 times ]
Length of side AB is 4, and the length of side BC is xand AC is between 4 and 8. There can be many triangles that satify this condition.
On one extreme when AC is almost 4. Then the the triangle becomes almost the line AB and \(x\) is almost 0.
On the other hand when AC is 8 then \(x=\sqrt{8^2-4^2} \approx 6.9\).
So all values from 0 to 6.9 form a right triangle. Hence all options are correct!
Show: :: img
Attachment:
right.jpg [ 13.28 KiB | Viewed 39407 times ]
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: In triangle ABC, the measure of angle B is 90°, the length o
[#permalink]
 12 Jul 2021, 05:40
12 Jul 2021, 05:40
3
Carcass wrote:
In triangle ABC, the measure of angle B is 90°, the length of side AB is 4, and the length of side BC is x. If the length of hypotenuse AC is between 4 and 8, which of the following could be the value of x ?
Indicate \(all\) such values.
❑ 1
❑ 2
❑ 3
❑ 4
❑ 5
❑ 6
Indicate \(all\) such values.
❑ 1
❑ 2
❑ 3
❑ 4
❑ 5
❑ 6
I would solve the question by testing each choice.
A) x = 1
The Pythagorean theorem tells us that 4² + 1² = hypotenuse²
Solve to get: Hypotenuse = √17
Since √17 is between 4 and 8, x COULD equal 1
B) x = 2
The Pythagorean theorem tells us that 4² + 2² = hypotenuse²
Solve to get: Hypotenuse = √20
Since √20 is between 4 and 8, x COULD equal 2
C) x = 3
The Pythagorean theorem tells us that 4² + 3² = hypotenuse²
Solve to get: Hypotenuse = √25
Since √25 is between 4 and 8, x COULD equal 3
D) x = 4
The Pythagorean theorem tells us that 4² + 4² = hypotenuse²
Solve to get: Hypotenuse = √32
Since √32 is between 4 and 8, x COULD equal 4
E) x = 5
The Pythagorean theorem tells us that 4² + 5² = hypotenuse²
Solve to get: Hypotenuse = √41
Since √41 is between 4 and 8, x COULD equal 5
F) x = 6
The Pythagorean theorem tells us that 4² + 6² = hypotenuse²
Solve to get: Hypotenuse = √52
Since √52 is between 4 and 8, x COULD equal 6
Answer: A, B, C, D, E and F










