GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
In the circle shown above O is the centre of the circle and AB is a ta
[#permalink]
10 May 2023, 05:03
10 May 2023, 05:03
Expert Reply
1
Bookmarks
00:00
Question Stats:
85% (01:27) correct
14% (02:06) wrong based on 7 sessions
Hide Show timer Statistics
Attachment:
GRE In the circle shown above O is the centre.jpg [ 12.59 KiB | Viewed 1505 times ]
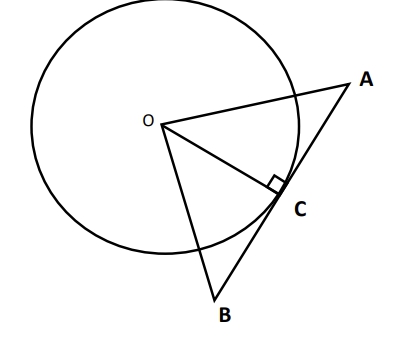
In the circle shown above O is the centre of the circle and AB is a tangent to the circle at C. If triangle AOB is an equilateral triangle and AB is 10cm, what is the area of the circle?
\(25 \pi\)
\(50 \pi\)
\(75 \pi\)
\(100 \pi\)
\(120 \pi\)
Post A Detailed Correct Solution For The Above Questions And Get Kudos.
Question From Our Project: Free GRE Prep Club Tests in Exchange for 20 Kudos
\(\Longrightarrow\) GRE - Quant Daily Topic-wise Challenge
\(\Longrightarrow\) GRE GEOMETRY
Re: In the circle shown above O is the centre of the circle and AB is a ta
[#permalink]
17 May 2023, 01:03
17 May 2023, 01:03
height of equilateral triangle is root 3 multiplied by side/2
Re: In the circle shown above O is the centre of the circle and AB is a ta
[#permalink]
27 May 2023, 09:23
27 May 2023, 09:23
1
Expert Reply
OE
We need to find the area of the circle cantered at O in the figure given.
GRE circle 5.jpg [ 26.31 KiB | Viewed 1303 times ]
If we join OC, then we can see that OC is the radius of the circle.
Also, we know that radius of a circle is perpendicular to the tangent.
Hence OC, radius of circle, is perpendicular to AB and is also
the height of equilateral triangle OAB.
We know,
Height of equilateral triangle = √3/2 ∗ 𝑠𝑖𝑑𝑒
Side of equilateral triangle OAB is given as 10cm.
OC = √3/2 × 10 = 5√3
Hence,
Area of circle = 𝜋(5√3)^2= 75 𝜋
Ans. (C)
We need to find the area of the circle cantered at O in the figure given.
Attachment:
GRE circle 5.jpg [ 26.31 KiB | Viewed 1303 times ]
If we join OC, then we can see that OC is the radius of the circle.
Also, we know that radius of a circle is perpendicular to the tangent.
Hence OC, radius of circle, is perpendicular to AB and is also
the height of equilateral triangle OAB.
We know,
Height of equilateral triangle = √3/2 ∗ 𝑠𝑖𝑑𝑒
Side of equilateral triangle OAB is given as 10cm.
OC = √3/2 × 10 = 5√3
Hence,
Area of circle = 𝜋(5√3)^2= 75 𝜋
Ans. (C)
