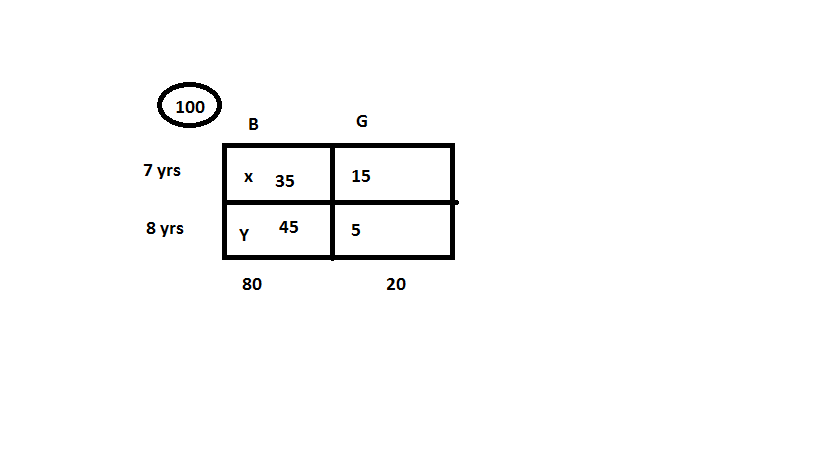
From the question stem draw out a double matrix. It is easier to solve with a double matrix rather than forming a equation.
Put two columns B for Boys and G for Girls
Put two rows 7 yrs for 7 yrs students and 8 yrs for 8 yrs students

Now take a nice number so that it is easier to work for Eg. 100 for total students.
Fill up the information:

Boys $(B) =\frac{80}{100} * 100 = 80$
Hence Girls$(G) = 20$

Now find the number of 8 yrs old girl $= 20 * \frac{25}{100} = 5$
From this find the number of girls who are 7 yrs old = $20-5 = 15$

Let x = number of boys that are 7 yrs old
and Y = number of boys that are 8 yrs old

Given,
$x + 15 = y + 5$
also we can deduce $x + y = 80$
solve the two pair of equation to find the value for x and y
$x = 35 and Y = 45$

Therefore, % of boys that are 7 yrs old is 35