GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
The figure belkow shoes an inscribed triangle
[#permalink]
08 Feb 2024, 00:56
08 Feb 2024, 00:56
Expert Reply
00:00
Question Stats:
100% (03:53) correct
0% (00:00) wrong based on 4 sessions
Hide Show timer Statistics
The figure below shows an inscribed triangle ABC in a circle. If AB=6, what is the combined area of the shaded regions
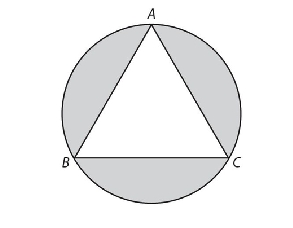
GRE circle geometry.jpg [ 15.7 KiB | Viewed 532 times ]
A. \(4 \pi - \sqrt{3 }\)
B. \(6 \pi - 6 \sqrt{3}\)
C. \(9 \pi - 4 \sqrt{3}\)
D. \(12 \pi - 9 \sqrt{3}\)
E. \(18 \pi - 16 \sqrt{3} \)
Attachment:
GRE circle geometry.jpg [ 15.7 KiB | Viewed 532 times ]
A. \(4 \pi - \sqrt{3 }\)
B. \(6 \pi - 6 \sqrt{3}\)
C. \(9 \pi - 4 \sqrt{3}\)
D. \(12 \pi - 9 \sqrt{3}\)
E. \(18 \pi - 16 \sqrt{3} \)
Part of the project: The Butler-GRE Daily New Quant and Verbal Questions to Practice (2023) - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
The figure belkow shoes an inscribed triangle
[#permalink]
15 Feb 2024, 15:00
15 Feb 2024, 15:00
1
First of all The question is wrong. Insufficient information.
The question should be stated as Equilateral triangle and thereafter,
The area of triangle inside of circle = (\sqrt{3}/4) * a^2 = (\sqrt{3}/4) * 36 = 9* \sqrt{3}
If we draw lines from centre of the circle to the two corner of given triangle it will form an isoscales triangle with radius both sides and 6 other side. Then we need to draw perpendicular line from base to the centre of the circle to create, 30:60:90 triangle.
With that we can calculate the radius of the circle, r = 6/ \sqrt{3}
total area of circle is = \pi * r^2 = 12 * \pi
area of shaded region = 12 * \pi - 9 * \sqrt{3}
D.
The question should be stated as Equilateral triangle and thereafter,
The area of triangle inside of circle = (\sqrt{3}/4) * a^2 = (\sqrt{3}/4) * 36 = 9* \sqrt{3}
If we draw lines from centre of the circle to the two corner of given triangle it will form an isoscales triangle with radius both sides and 6 other side. Then we need to draw perpendicular line from base to the centre of the circle to create, 30:60:90 triangle.
With that we can calculate the radius of the circle, r = 6/ \sqrt{3}
total area of circle is = \pi * r^2 = 12 * \pi
area of shaded region = 12 * \pi - 9 * \sqrt{3}
D.
gmatclubot
The figure belkow shoes an inscribed triangle [#permalink]
15 Feb 2024, 15:00
Moderators:
