GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
What is the perimeter of the quadrilateral shown above?
[#permalink]
11 Jan 2025, 00:37
11 Jan 2025, 00:37
Expert Reply
00:00
Question Stats:
100% (01:26) correct
0% (00:00) wrong based on 1 sessions
Hide Show timer Statistics
Attachment:
GRE geometry practice question.png [ 17.33 KiB | Viewed 217 times ]
(A) $\((4 \sqrt{2}) x\)$
(B) $\((4+\sqrt{2}) x\)$
(C) $\((4+2 \sqrt{2}) x\)$
(D) $\(5 x\)$
(E) $\(6 x\)$
- Part of the project: GRE Quant & Verbal ADVANCED Daily Challenge 2024 Edition - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
- Also replying to the unanswered questions
What is the perimeter of the quadrilateral shown above?
[#permalink]
19 Feb 2025, 11:22
19 Feb 2025, 11:22
Expert Reply
OFFICIAL EXPLANATION
GRE parallelogram (2).png [ 101.49 KiB | Viewed 42 times ]
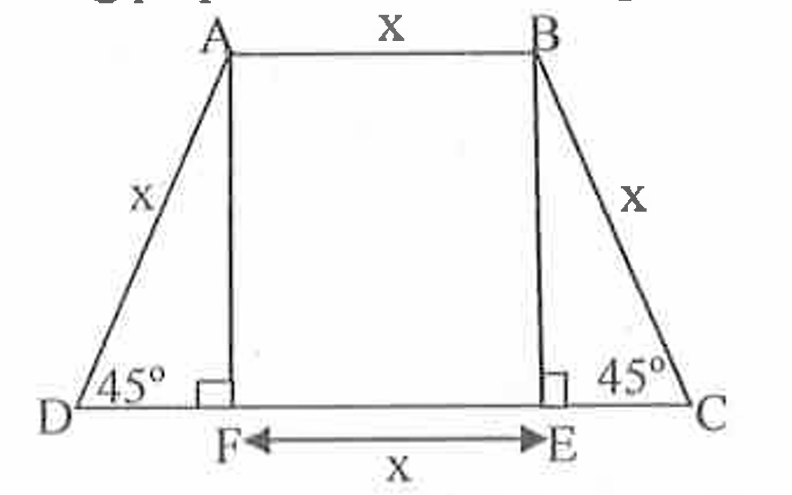
In one of the isosceles right triangle in the figure, say triangle $\(A D F\)$, let the base $\(=D F=\mathrm{k}=$ height $=A F\)$, so applying Pythagoras theorem, we get $\(k^2+k^2=x^2\)$
i.e. $\(2 \mathrm{k}^2=\mathrm{x}^2 \Rightarrow \mathrm{k}=\frac{x}{\sqrt{2}}\)$ which is the value of two identical bases $\((=\mathrm{DF}=\mathrm{EC})\)$ of two isosceles right triangles \(ADF \& BEC.\) \((Pythagoras theorem - Hypotenuse ${ }^2=\)$ Perpendicular $\(^2+\)$ Base $\(^2\)$ )
Finally the perimeter of the trapezium is $\(\mathrm{AB}+\mathrm{BC}+\mathrm{FE}+\mathrm{AD}+\mathrm{DF}+\mathrm{EC}=\)$ $\(x+x+x+x+\frac{x}{\sqrt{2}}+\frac{x}{\sqrt{2}}=4 x+\sqrt{2} x=(4+\sqrt{2}) x\)$
Hence the answer is (B).
Attachment:
GRE parallelogram (2).png [ 101.49 KiB | Viewed 42 times ]
In one of the isosceles right triangle in the figure, say triangle $\(A D F\)$, let the base $\(=D F=\mathrm{k}=$ height $=A F\)$, so applying Pythagoras theorem, we get $\(k^2+k^2=x^2\)$
i.e. $\(2 \mathrm{k}^2=\mathrm{x}^2 \Rightarrow \mathrm{k}=\frac{x}{\sqrt{2}}\)$ which is the value of two identical bases $\((=\mathrm{DF}=\mathrm{EC})\)$ of two isosceles right triangles \(ADF \& BEC.\) \((Pythagoras theorem - Hypotenuse ${ }^2=\)$ Perpendicular $\(^2+\)$ Base $\(^2\)$ )
Finally the perimeter of the trapezium is $\(\mathrm{AB}+\mathrm{BC}+\mathrm{FE}+\mathrm{AD}+\mathrm{DF}+\mathrm{EC}=\)$ $\(x+x+x+x+\frac{x}{\sqrt{2}}+\frac{x}{\sqrt{2}}=4 x+\sqrt{2} x=(4+\sqrt{2}) x\)$
Hence the answer is (B).
gmatclubot
What is the perimeter of the quadrilateral shown above? [#permalink]
19 Feb 2025, 11:22
Moderators:
