A median value of any probability distribution divides the area under the probabaility distribution in two equal parts.
Best understood with following image.
Now in our case we need to split the triangular distribution along a line \(x=?\) (parallel to y axis) such that area of the right half is same as the left half.

Area of right half = \(\frac{1}{2} \times\) Area of the larger triangle.
Now look at the figure below and we have marked out the hight and length of the triangle as x. Now height = length for this triangle because the given line has slope 1.

Area of right half = \(\frac{1}{2} \times x^2\)= \(\frac{1}{2} \times \frac{1}{2}\times \sqrt{2}^2\).
Solving for x we get x =1. So median value has to be \(\sqrt{2}-1\) (refer to the figure above)
Attachment:
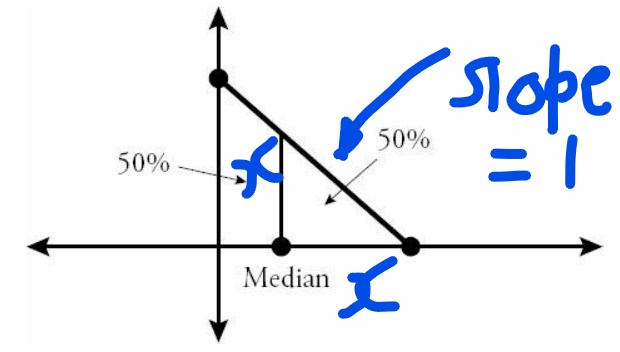 Inkedtriangle_LI.jpg [ 841.95 KiB | Viewed 18716 times ]
Inkedtriangle_LI.jpg [ 841.95 KiB | Viewed 18716 times ]
Attachment:
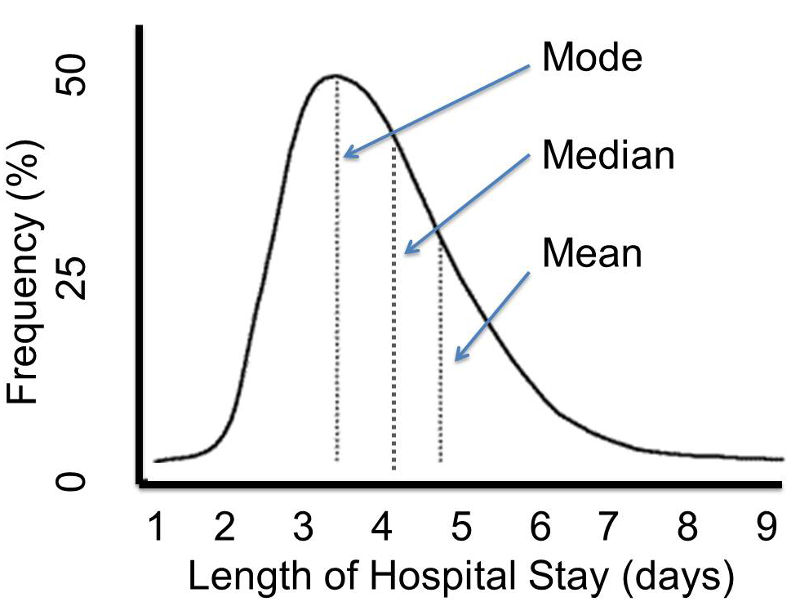
 Skewed.png [ 131.58 KiB | Viewed 18759 times ]
Skewed.png [ 131.58 KiB | Viewed 18759 times ]








 26% (02:41) correct
26% (02:41) correct






