GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
All of the students in a certain class are either 7 or 8 yea
[#permalink]
18 Mar 2018, 06:37
18 Mar 2018, 06:37
1
Expert Reply
2
Bookmarks
00:00
Question Stats:
81% (02:00) correct
18% (02:21) wrong based on 27 sessions
Hide Show timer Statistics
All of the students in a certain class are either 7 or 8 years old. 80 percent of the students are boys and 25 percent of the girls are 8 years old. If there are an equal number of 7-year-olds and 8-year-olds, what percent of the students in the class are boys who are 7 years old?
Drill 2
Question: 13
Page: 499
Question: 13
Page: 499
Show: :: OA
35
Re: All of the students in a certain class are either 7 or 8 yea
[#permalink]
20 Mar 2018, 09:16
20 Mar 2018, 09:16
1
1
Bookmarks
From the question stem draw out a double matrix. It is easier to solve with a double matrix rather than forming a equation.
Put two columns B for Boys and G for Girls
Put two rows 7 yrs for 7 yrs students and 8 yrs for 8 yrs students
Now take a nice number so that it is easier to work for Eg. 100 for total students.
Fill up the information:
Boys \((B) =\frac{80}{100} * 100 = 80\)
Hence Girls\((G) = 20\)
Now find the number of 8 yrs old girl \(= 20 * \frac{25}{100} = 5\)
From this find the number of girls who are 7 yrs old = \(20-5 = 15\)
Let x = number of boys that are 7 yrs old
and Y = number of boys that are 8 yrs old
Given,
\(x + 15 = y + 5\)
also we can deduce \(x + y = 80\)
solve the two pair of equation to find the value for x and y
\(x = 35 and Y = 45\)
Therefore, % of boys that are 7 yrs old is 35
Put two columns B for Boys and G for Girls
Put two rows 7 yrs for 7 yrs students and 8 yrs for 8 yrs students
Now take a nice number so that it is easier to work for Eg. 100 for total students.
Fill up the information:
Boys \((B) =\frac{80}{100} * 100 = 80\)
Hence Girls\((G) = 20\)
Now find the number of 8 yrs old girl \(= 20 * \frac{25}{100} = 5\)
From this find the number of girls who are 7 yrs old = \(20-5 = 15\)
Let x = number of boys that are 7 yrs old
and Y = number of boys that are 8 yrs old
Given,
\(x + 15 = y + 5\)
also we can deduce \(x + y = 80\)
solve the two pair of equation to find the value for x and y
\(x = 35 and Y = 45\)
Therefore, % of boys that are 7 yrs old is 35
Attachments
ans.png [ 5.97 KiB | Viewed 4090 times ]
Re: All of the students in a certain class are either 7 or 8 yea
[#permalink]
21 Mar 2018, 14:04
21 Mar 2018, 14:04
1
Expert Reply
Explanation
Wouldn’t this be a lot easier if you knew how many students there are?
The question doesn’t say, so plug in your own number.
The question deals in percentages, so let’s say there are 100 students in the class. That means that there are 80 boys and 20 girls, and 50 students who are 7 and 50 students who are 8. 25 percent of 20 is 5, which leaves 15 girls who are 7.
Subtract 15 from 50 and you are left with 35 boys who are 7. You can also employ the group grid.
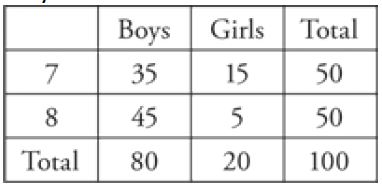
Capture.JPG [ 19.04 KiB | Viewed 4083 times ]
Wouldn’t this be a lot easier if you knew how many students there are?
The question doesn’t say, so plug in your own number.
The question deals in percentages, so let’s say there are 100 students in the class. That means that there are 80 boys and 20 girls, and 50 students who are 7 and 50 students who are 8. 25 percent of 20 is 5, which leaves 15 girls who are 7.
Subtract 15 from 50 and you are left with 35 boys who are 7. You can also employ the group grid.
Attachment:
Capture.JPG [ 19.04 KiB | Viewed 4083 times ]
