
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Director

Joined: 16 May 2014
Posts: 592
Given Kudos: 0
GRE 1: Q165 V161
Quant: Number Theory
[#permalink]
 21 Jun 2016, 06:01
21 Jun 2016, 06:01
3
Expert Reply
1
Bookmarks
Number Theory:
This post is written with the motivation to be a one-stop shop of all number theory concepts you may have to use during your GRE exam. Please feel free to suggest if I missed out on something.
Definition
Number Theory is concerned with the properties of numbers in general, and in particular integers. As this is a huge issue we decided to divide it into smaller topics. Below is the list of Number Theory topics.
GRE Number Types
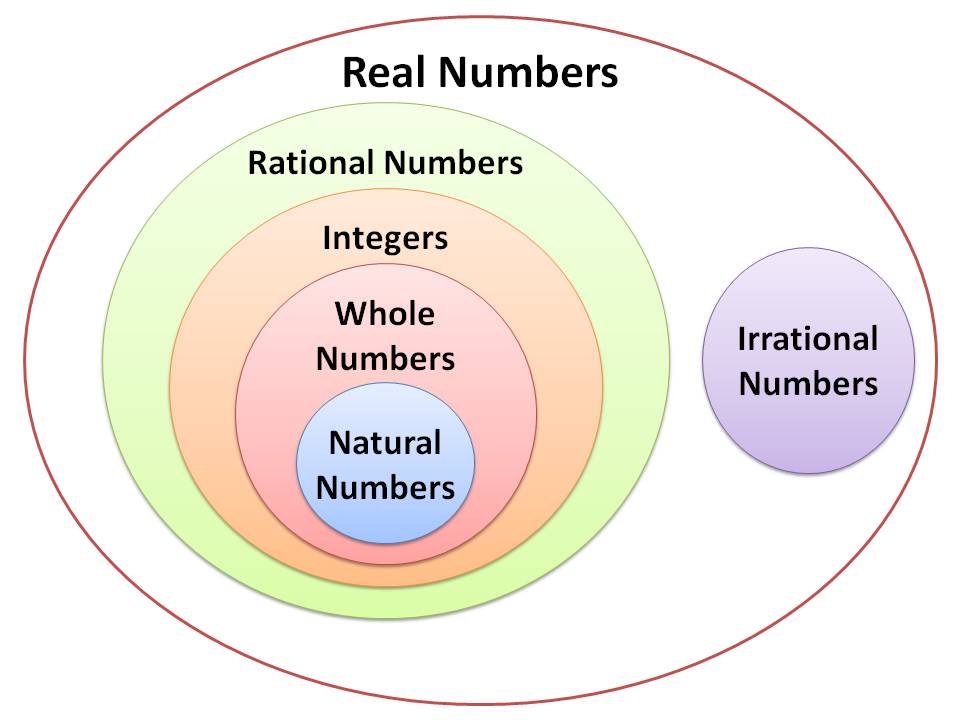
GRE deals with only Real Numbers: Integers, Fractions and Irrational Numbers. In the following paragraphs we discuss the individual types.
Integers
Integers are defined as: all negative natural numbers {...,−4,−3,−2,−1}, zero {0}, and positive natural numbers {1,2,3,4,...}.
Note that integers do not include decimals or fractions - just whole numbers.
Even and Odd Numbers
An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without a remainder.
An even number is an integer of the form n=2kn=2k, where kk is an integer.
An odd number is an integer that is not evenly divisible by 2.
An odd number is an integer of the form n=2k+1n=2k+1, where kk is an integer.
Zero is an even number.
Addition / Subtraction:
even +/- even = even;
even +/- odd = odd;
odd +/- odd = even.
Multiplication:
even * even = even;
even * odd = even;
odd * odd = odd.
Division of two integers can result into an even/odd integer or a fraction.
IRRATIONAL NUMBERS
Fractions (also known as rational numbers) can be written as terminating (ending) or repeating decimals (such as 0.5, 0.76, or 0.333333....). On the other hand, all those numbers that can be written as non-terminating, non-repeating decimals are non-rational, so they are called the "irrationals". Examples would be 2√2 ("the square root of two") or the number pi (π=π=~3.14159..., from geometry). The rationals and the irrationals are two totally separate number types: there is no overlap.
Putting these two major classifications, the rationals and the irrationals, together in one set gives you the "real" numbers.
POSITIVE AND NEGATIVE NUMBERS
A positive number is a real number that is greater than zero.
A negative number is a real number that is smaller than zero.
Zero is not positive, nor negative.
Multiplication:
positive * positive = positive
positive * negative = negative
negative * negative = positive
Division:
positive / positive = positive
positive / negative = negative
negative / negative = positive
Prime Numbers
A Prime number is a natural number with exactly two distinct natural number divisors: 1 and itself. Otherwise a number is called a composite number. Therefore, 1 is not a prime, since it only has one divisor, namely 1. A number n>1 is prime if it cannot be written as a product of two factors aa and bb, both of which are greater than 1: n = ab.
- The first twenty-six prime numbers are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101 - Note: only positive numbers can be primes.
- There are infinitely many prime numbers.
- The only even prime number is 2, since any larger even number is divisible by 2. Also 2 is the smallest prime.
- All prime numbers except 2 and 5 end in 1, 3, 7 or 9, since numbers ending in 0, 2, 4, 6 or 8 are multiples of 2 and numbers ending in 0 or 5 are multiples of 5. Similarly, all prime numbers above 3 are of the form 6n−1 or 6n+1, because all other numbers are divisible by 2 or 3.
- Any nonzero natural number n can be factored into primes, written as a product of primes or powers of primes. Moreover, this factorization is unique except for a possible reordering of the factors.
- Prime factorization: every positive integer greater than 1 can be written as a product of one or more prime integers in a way which is unique. For instance integer n with three unique prime factors a, b, and c can be expressed as \(n=a^p * b^q * c^r\), where p, q, and r are powers of a, b, and c, respectively and are ≥1.
Example: \(4200\)=\(2^3\)∗\(3\)∗\(5^2\)∗\(7\). - Verifying the primality (checking whether the number is a prime) of a given number nn can be done by trial division, that is to say dividing n by all integer numbers smaller than \(\sqrt{n}\), thereby checking whether n is a multiple of m≤\(\sqrt{n}\).
Example: Verifying the primality of 161: √161 is little less than 13, from integers from 2 to 13, 161 is divisible by 7, hence 161 is not prime.
Note that, it is only necessary to try dividing by prime numbers up to √n, since if n has any divisors at all (besides 1 and n), then it must have a prime divisor. - If \(n\) is a positive integer greater than 1, then there is always a prime number p with \(n<p<2n\).
Factors
A divisor of an integer n, also called a factor of n, is an integer which evenly divides n without leaving a remainder. In general, it is said m is a factor of n, for non-zero integers m and n, if there exists an integer k such that n=km.
- 1 (and -1) are divisors of every integer.
- Every integer is a divisor of itself.
- Every integer is a divisor of 0, except, by convention, 0 itself.
- Numbers divisible by 2 are called even and numbers not divisible by 2 are called odd.
- A positive divisor of n which is different from n is called a proper divisor.
- An integer n > 1 whose only proper divisor is 1 is called a prime number. Equivalently, one would say that a prime number is one which has exactly two factors: 1 and itself.
- Any positive divisor of n is a product of prime divisors of n raised to some power.
- If a number equals the sum of its proper divisors, it is said to be a perfect number.
Example: The proper divisors of 6 are 1, 2, and 3: 1+2+3=6, hence 6 is a perfect number.
There are some elementary rules: - If a is a factor of b and a is a factor of c, then a is a factor of (b+c). In fact, a is a factor of (mb+nc) for all integers m and n.
- If a is a factor of b and b is a factor of c, then a is a factor of c.
- If a is a factor of b and b is a factor of a, then a=b or a=−b.
- If a is a factor of bc, and gcd(a,b)=1, then a is a factor of c.
- If p is a prime number and p is a factor of ab then p is a factor of a or p is a factor of b.
Finding the Number of Factors of an Integer
First make prime factorization of an integer \(n=a^p * b^q * c^r\), where a, b, and c are prime factors of n and p, q, and r are their powers.
The number of factors of n will be expressed by the formula \((p+1)(q+1)(r+1)\). NOTE: this will include 1 and n itself.
Example: Finding the number of all factors of 450: \(450 = 2^1*3^2*5^2\)
Total number of factors of 450 including 1 and 450 itself is (1+1)∗(2+1)∗(2+1)=2 ∗ 3 ∗ 3=18 factors.
Finding the Sum of the Factors of an Integer
First make prime factorization of an integer \(n=a^p * b^q * c^r\), where a, b, and c are prime factors of n and p, q, and r are their powers.
The sum of factors of n will be expressed by the formula: \(\frac{( a^{p+1} - 1) * ( b^{q+1} - 1) * ( c^{r+1}-1)}{(a-1) * (b-1) * (c-1)}\)
Example: Finding the sum of all factors of 450: \(450= 2^1*3^2*5^2\).
The sum of all factors of 450 is \(\frac{(2^{1+1} - 1)*(3^{2+1} - 1)*(5^{2+1}-1)}{(2-1)*(3-1)*(5-1)}=\frac{3*26*124}{1*2*4} = 1209\)
Re: Quant: Number Theory
[#permalink]
 24 Feb 2021, 20:22
24 Feb 2021, 20:22
Hello from the GRE Prep Club BumpBot!
Thanks to another GRE Prep Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).
Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.
Thanks to another GRE Prep Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).
Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.

gmatclubot
Re: Quant: Number Theory [#permalink]
24 Feb 2021, 20:22
Moderators:


