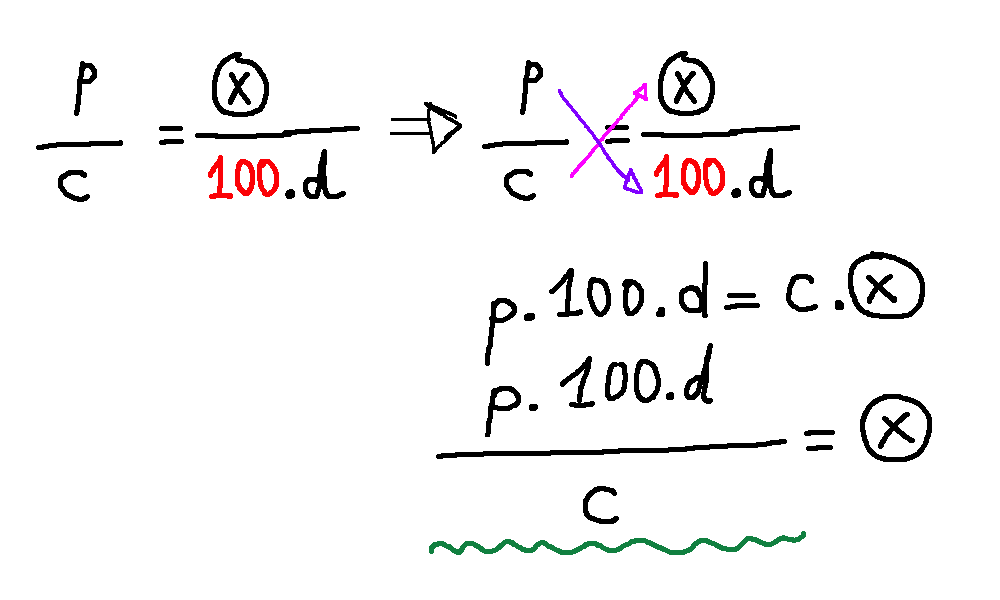GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If p pencils cost c cents at the same rate, how many
[#permalink]
 16 May 2017, 07:59
16 May 2017, 07:59
Expert Reply
4
Bookmarks
Question Stats:
 61% (01:13) correct
61% (01:13) correct
 38% (01:12) wrong
38% (01:12) wrong  based on 181 sessions
based on 181 sessions
Hide Show timer Statistics
If p pencils cost c cents at the same rate, how many pencils can be bought for d dollars?
A) \(cdp\)
B) \(100 cdp\)
C) \(\frac{dp}{100c}\)
D) \(\frac{100cd}{p}\)
E) \(\frac{100 dp}{c}\)
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: If p pencils cost c cents at the same rate, how many
[#permalink]
 18 May 2017, 13:04
18 May 2017, 13:04
3
1
Bookmarks
Carcass wrote:
If p pencils cost c cents at the same rate, how many pencils can be bought for d dollars?
A) \(cdp\)
B) \(100 cdp\)
C) \(\frac{dp}{100c}\)
D) \(\frac{100cd}{p}\)
E) \(\frac{100 dp}{c}\)
These kinds of questions (Variables in the Answer Choices - VIACs) can be answered algebraically or using the INPUT-OUTPUT approach.
Let's use the INPUT-OUTPUT approach.
Pick some numbers that meet the given information.
Say p = 3 and c = 50
This means that we can buy 3 pencils for 50 cents ($0.50)
Let's also say that d = 1
This means that the question is now asking "How many pencils can be bought for 1 dollar"
If we can buy 3 pencils for 50 cents, then we can buy 6 pencils for 1 dollar
So, when p = 3, c = 50 and d = 1, the answer to our question is 6 pencils.
Now let's take each answer choice and see which one yields an OUTPUT of 6, when we input p = 3, c = 50 and d = 1
A) cdp = (50)(1)(3) = 150. We need an output of 6. ELIMINATE.
B) 100cdp = (100)(50)(1)(3) = 15000. We need an output of 6. ELIMINATE.
C) dp/100c = (1)(3)/(100)(50) = 3/5000. We need an output of 6. ELIMINATE.
D) 100cd/p = (100)(50)(1)/(3) = 5000/3. We need an output of 6. ELIMINATE.
E) 100dp/c = (100)(1)(3)/(50) = 6. BINGO!
Answer:
Show: ::
E
Re: If p pencils cost c cents at the same rate, how many
[#permalink]
 17 Sep 2018, 00:41
17 Sep 2018, 00:41
1
Step 1 - pc - p pencils* c cents
step 2 - p pencils into d dollars --> d dollars to cents --100d
divided by no of cents --> 100pd/ c
step 2 - p pencils into d dollars --> d dollars to cents --100d
divided by no of cents --> 100pd/ c