GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
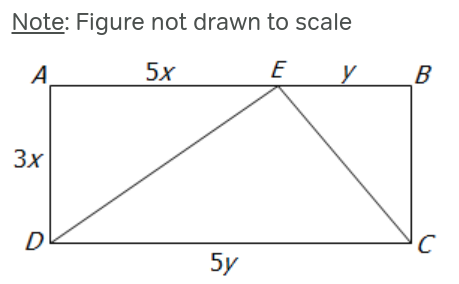
If AD = 3x, AE = 5x, EB = y and DC = 5y, what is the ratio o
[#permalink]
02 Feb 2020, 09:31
02 Feb 2020, 09:31
00:00
Question Stats:
0% (00:00) correct
100% (02:44) wrong based on 1 sessions
Hide Show timer Statistics
If AD = 3x, AE = 5x, EB = y and DC = 5y, what is the ratio of the area of triangle DEC to the area of rectangle ABCD ?
Screenshot from 2020-02-02 23-29-52.png [ 25.07 KiB | Viewed 1834 times ]
A. 2:7
B. 1:3
C. 2:5
D. 1:2
E. 3:5
Attachment:
Screenshot from 2020-02-02 23-29-52.png [ 25.07 KiB | Viewed 1834 times ]
A. 2:7
B. 1:3
C. 2:5
D. 1:2
E. 3:5
GRE Instructor
Joined: 19 Jan 2020
Status:Entrepreneur | GMAT, GRE, CAT, SAT, ACT coach & mentor | Founder @CUBIX | Edu-consulting | Content creator
Posts: 117
Given Kudos: 0
GPA: 3.72
Re: If AD = 3x, AE = 5x, EB = y and DC = 5y, what is the ratio o
[#permalink]
02 Feb 2020, 11:30
02 Feb 2020, 11:30
huda wrote:
If AD = 3x, AE = 5x, EB = y and DC = 5y, what is the ratio of the area of triangle DEC to the area of rectangle ABCD ?
A. 2:7
B. 1:3
C. 2:5
D. 1:2
E. 3:5
Attachment:
Screenshot from 2020-02-02 23-29-52.png
A. 2:7
B. 1:3
C. 2:5
D. 1:2
E. 3:5
In this question, you can always do the following:
Step 1: Find area of rectangle ABCD in terms of x (Use AB = 5x + y = CD = 5y)
Step 2: Find area of triangle AED in terms of x
Step 3: Find area of triangle BEC in terms of x (Use BC = AD = 3x)
Step 4: Subtract areas of AED and BEC from ABCD to find area of triangle DEC
Step 5: Find required ratio
However, there is a way simpler method:
Area of triangle DEC = 1/2 * Base * Height = 1/2 * CD * AD = 1/2 * Area of ABCD
(Note: Height of the triangle = height of the rectangle = AD)
Thus, required ratio of the triangle to the rectangle = 1 : 2
Answer D
gmatclubot
Re: If AD = 3x, AE = 5x, EB = y and DC = 5y, what is the ratio o [#permalink]
02 Feb 2020, 11:30
Moderators:
