GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
How many roots
[#permalink]
04 Nov 2019, 22:43
04 Nov 2019, 22:43
1
1
4
Bookmarks
00:00
Question Stats:
50% (01:36) correct
50% (01:48) wrong based on 18 sessions
Hide Show timer Statistics
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: How many roots
[#permalink]
28 Nov 2019, 10:33
28 Nov 2019, 10:33
1
Asmakan wrote:
How many roots does the equation \(\sqrt{x^2+1}+\sqrt{x^2+2}=2\) have?
Answer:
Show: ::
Question ID: Q02-08
My question: in the explanation, they solve it by substituting zero, why?
My question: in the explanation, they solve it by substituting zero, why?
Answer:
Show: ::
0
Key concept: \(x^2\) will always be greater than or equal to 0.
So, the smallest possible value of \(x^2 + 1\) is \(1\)
This occurs when \(x = 0\)
This means that the smallest possible value of \(\sqrt{x^2+1}\) is 1
Applying the same logic, we can see that the smallest possible value of \(x^2 + 2\) is \(2\)
This means that the smallest possible value of \(\sqrt{x^2+2}\) is \(\sqrt{2}\)
Since \(\sqrt{2} ≈ 1.4\), the smallest possible value of \(\sqrt{x^2+1}+\sqrt{x^2+2}\) ≈ 1 + 1.4 ≈ 2.4
This means it's impossible to have a solution to the equation \(\sqrt{x^2+1}+\sqrt{x^2+2}=2\)
In other words there are no solutions to that equation
Answer: 0
Cheers,
Brent
Re: How many roots
[#permalink]
30 May 2020, 12:05
30 May 2020, 12:05
1
A root of an equation is defined as the x intercept(s) of that equation. SO, this is wherever the graphed line intersects with the x axis, the values for which y=0 and x= something(s).
I've got an unconventional way to think about this problem.
Ignore the square roots on this problem for a second. Just imagine they weren't there. Here's what that graph would look like:
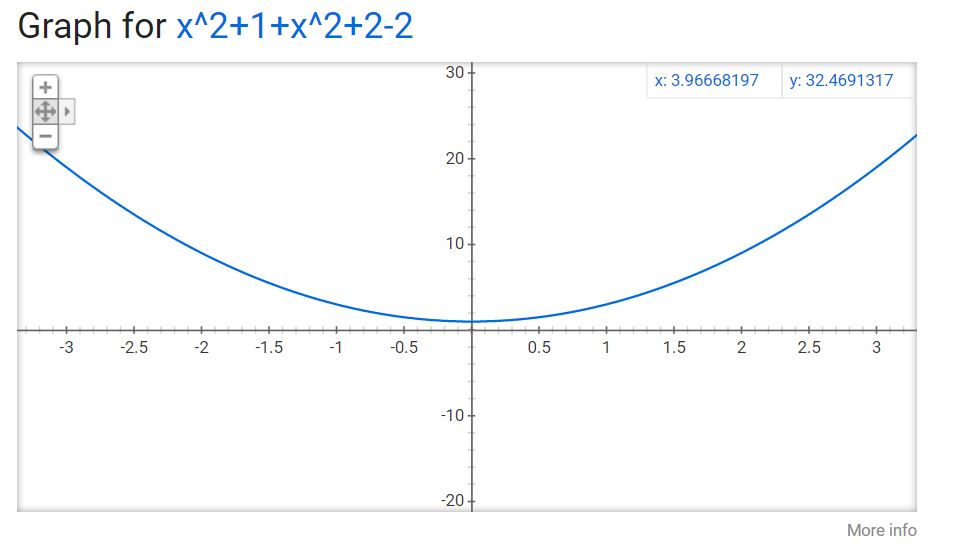
captureA.JPG [ 42.08 KiB | Viewed 2190 times ]
Now, if you add the square roots back into the equation, you're STILL not going to hit that x axis, because if you read the detailed explanation in Greenlighttestprep's answer, there is no real value for which you can manipulate any version of "x^2+1" to hit the x-axis. The "+1" in an equation this simple raises all the values so that there are no intercepts with the x axis.
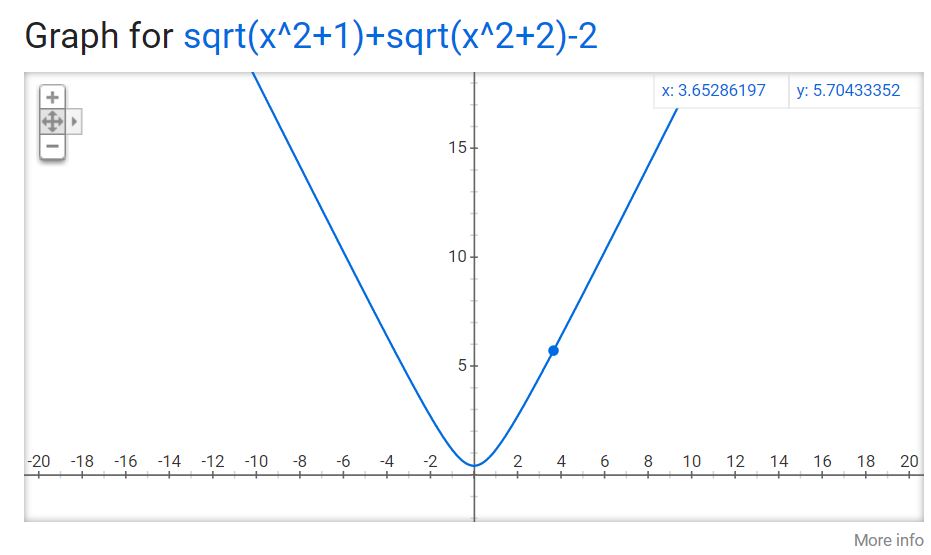
captureB.JPG [ 43.75 KiB | Viewed 2165 times ]
I've got an unconventional way to think about this problem.
Ignore the square roots on this problem for a second. Just imagine they weren't there. Here's what that graph would look like:
Attachment:
captureA.JPG [ 42.08 KiB | Viewed 2190 times ]
Now, if you add the square roots back into the equation, you're STILL not going to hit that x axis, because if you read the detailed explanation in Greenlighttestprep's answer, there is no real value for which you can manipulate any version of "x^2+1" to hit the x-axis. The "+1" in an equation this simple raises all the values so that there are no intercepts with the x axis.
Attachment:
captureB.JPG [ 43.75 KiB | Viewed 2165 times ]
