
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
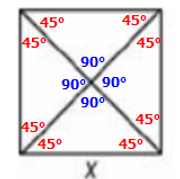
Figures X and Y above show how eight identical triangular pi
[#permalink]
 11 Jun 2020, 09:03
11 Jun 2020, 09:03
Expert Reply
3
Bookmarks
Question Stats:
 64% (01:47) correct
64% (01:47) correct
 35% (00:56) wrong
35% (00:56) wrong  based on 42 sessions
based on 42 sessions
Hide Show timer Statistics
Figures X and Y above show how eight identical triangular pieces of cardboard were used to form a square and a rectangle, respectively. What is the ratio of the perimeter of X to the perimeter of Y?
(A) 2:3
(B) \(\sqrt{2}:2\)
(C) \(2\sqrt{2} :3\)
(D) 1:1
(E) \(\sqrt{2}:1\)
Re: Figures X and Y above show how eight identical triangular pi
[#permalink]
 11 Jun 2020, 09:03
11 Jun 2020, 09:03
Expert Reply
Post A Detailed Correct Solution For The Above Questions And Get A Kudos.
Question From Our New Project: GRE Quant Challenge Questions Daily - NEW EDITION!
Question From Our New Project: GRE Quant Challenge Questions Daily - NEW EDITION!
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: Figures X and Y above show how eight identical triangular pi
[#permalink]
 11 Jun 2020, 09:13
11 Jun 2020, 09:13
2
1
Bookmarks
Carcass wrote:
Figures X and Y above show how eight identical triangular pieces of cardboard were used to form a square and a rectangle, respectively. What is the ratio of the perimeter of X to the perimeter of Y?
(A) 2:3
(B) \(\sqrt{2}:2\)
(C) \(2\sqrt{2} :3\)
(D) 1:1
(E) \(\sqrt{2}:1\)
Let's start by gathering more information about these eight identical triangles.
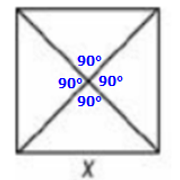
First notice that we have 4 equal angles meeting at a single point.
So, each angle must be 90°
Now examine the red triangle below.
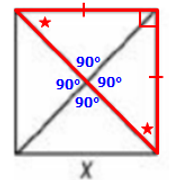
The red triangle is an isosceles triangle since all 4 sides of a square are equal.
The two equal angles must add to 90°
So, each angle must be 45°
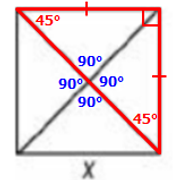
Using similar logic, we can conclude that all of the eight triangles are 45-45-90 special right triangles.
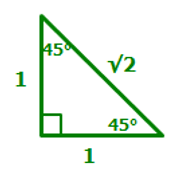
Now let's examine what happens if we examine one particular 45-45-90 special right triangle, which has sides of length 1, 1 and √2
Use those lengths for all eight identical triangles in the 2 diagrams we get the following:
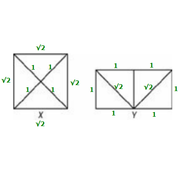
At this point, we can calculate the perimeters.
Perimeter of X = √2 + √2 + √2 + √2 = 4√2
Perimeter of Y = 1 + 1 + 1 + 1 + 1 + 1 = 6
So, perimeter of X : perimeter of Y = 4√2 : 6
Divide both sides by 2 to get the equivalent ratio 2√2 : 3
Answer: C
ASIDE: Please note that I didn't have to use those specific lengths (1, 1 and √2) for each of the 45-45-90 triangles.
I could have used ANY measurements that could be found in a 45-45-90 triangle.
For example, I could have used 5, 5 and 5√2, and those measurements still would have yielded the same ratio (after some simplifying)
Cheers,
Brent





