
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Retired Moderator
Joined: 16 Apr 2020
Status:Founder & Quant Trainer
Affiliations: Prepster Education
Posts: 1546
Given Kudos: 172
Location: India
WE:Education (Education)
An equilateral triangle PAB is inscribed inside a square PQRS, forming
[#permalink]
 05 Sep 2021, 22:25
05 Sep 2021, 22:25
1
7
Bookmarks
Question Stats:
 29% (02:56) correct
29% (02:56) correct
 70% (02:30) wrong
70% (02:30) wrong  based on 17 sessions
based on 17 sessions
Hide Show timer Statistics
An equilateral triangle PAB is inscribed inside a square PQRS, forming 3 right angled triangles - PQA, ARB and BSP.
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Quantity A |
Quantity B |
\(\frac{Area(△ARB)}{Area(△PQA)}\) |
\(\frac{4}{3}\) |
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Manager

Joined: 11 Nov 2023
Posts: 228
Given Kudos: 78
WE:Business Development (Advertising and PR)
An equilateral triangle PAB is inscribed inside a square PQRS, forming
[#permalink]
 29 Jan 2024, 19:29
29 Jan 2024, 19:29
1
This one's a doozy! Here's an illustration of the described triangle PAB inscribed inside square PQRS.
- Point B divides side QR such that \(SB = w\) and \(RB = r\) and the sides of the square are r + w.
\(Area(△PQA) = \frac{1}{2}*w*(r+w) = \frac{1}{2}(w^2 + rw)\)
- Since sides PA and PB are equal (bc they're sides of an equilateral triangle), and sides QR and SR are both r+w (bc they're sides of a square), their 3rd sides must also be equal. SB = QA = w
This means BR = r, so ARB is a 45-45-90 triangle. The hypotenuse of a 45-45-90 triangle is = its side length *\( \sqrt{2} \), so \(AB = r * \sqrt{2} \).
\(Area(△ARB) = \frac{1}{2}r^2\)
- AP is the hypotenuse of PQA. Since we found one of the sides of the equilateral triangle = \(r*\sqrt{2} \), we can set up the Pythagorean formula:
\(AQ^2 + QP^2 = AP^2\)
\(w^2 + (r+w)^2 = {r*\sqrt{2}}^2 \)
\(w^2 + r^2+2rw+w^2 = 2r^2\)
\(2w^2 +2rw = r^2\)
Thus, we can substitute \(2w^2 +2rw\) for \(r^2\).
\(\frac {Area of ARB}{Area of PQA} \frac\)
\(= \frac {\frac{1}{2}r^2} {\frac{1}{2}(w^2 + rw)} \frac \)
\(=\frac {2w^2 +2rw}{w^2 + rw}\frac \)
\(=2\)
Attachment:
File comment: Illustration of triangle PAB inscribed inside square PQRS
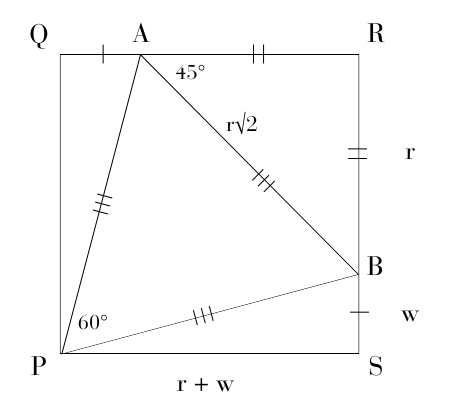
inscribed_triangle.png [ 21.19 KiB | Viewed 1715 times ]
inscribed_triangle.png [ 21.19 KiB | Viewed 1715 times ]
- Point B divides side QR such that \(SB = w\) and \(RB = r\) and the sides of the square are r + w.
\(Area(△PQA) = \frac{1}{2}*w*(r+w) = \frac{1}{2}(w^2 + rw)\)
- Since sides PA and PB are equal (bc they're sides of an equilateral triangle), and sides QR and SR are both r+w (bc they're sides of a square), their 3rd sides must also be equal. SB = QA = w
This means BR = r, so ARB is a 45-45-90 triangle. The hypotenuse of a 45-45-90 triangle is = its side length *\( \sqrt{2} \), so \(AB = r * \sqrt{2} \).
\(Area(△ARB) = \frac{1}{2}r^2\)
- AP is the hypotenuse of PQA. Since we found one of the sides of the equilateral triangle = \(r*\sqrt{2} \), we can set up the Pythagorean formula:
\(AQ^2 + QP^2 = AP^2\)
\(w^2 + (r+w)^2 = {r*\sqrt{2}}^2 \)
\(w^2 + r^2+2rw+w^2 = 2r^2\)
\(2w^2 +2rw = r^2\)
Thus, we can substitute \(2w^2 +2rw\) for \(r^2\).
\(\frac {Area of ARB}{Area of PQA} \frac\)
\(= \frac {\frac{1}{2}r^2} {\frac{1}{2}(w^2 + rw)} \frac \)
\(=\frac {2w^2 +2rw}{w^2 + rw}\frac \)
\(=2\)
General Discussion
Re: An equilateral triangle PAB is inscribed inside a square PQRS, forming
[#permalink]
 07 Sep 2021, 08:28
07 Sep 2021, 08:28
KarunMendiratta wrote:
An equilateral triangle PAB is inscribed inside a square PQRS, forming 3 right angled triangles - PQA, ARB and BSP.
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Quantity A |
Quantity B |
\(\frac{Area(△ARB)}{Area(△PQA)}\) |
\(\frac{4}{3}\) |
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Answer please !





